题目内容
若正数项数列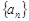 的前
的前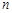 项和为
项和为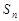 ,首项
,首项 ,点
,点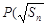 ,
,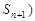 在曲线
在曲线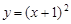 上.
上.
(1)求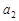 ,
,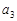 ;
;
(2)求数列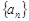 的通项公式
的通项公式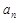 ;
;
(3)设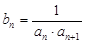 ,
,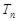 表示数列
表示数列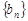 的前项和,若
的前项和,若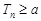 恒成立,求
恒成立,求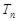 及实数
及实数 的取值范围.
的取值范围.
(1)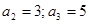 ;(2)
;(2)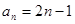 ;(3)
;(3) .
.
解析试题分析:(1)根据已知点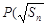 ,
,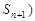 在曲线
在曲线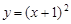 上,代入曲线,得到
上,代入曲线,得到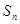 与
与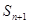 的关系,再根据
的关系,再根据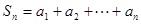 ,分别取
,分别取 和
和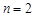 代入关系式,得到关于
代入关系式,得到关于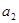 与
与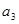 的方程组,解方程,得到结果;(2)由(1)得的
的方程组,解方程,得到结果;(2)由(1)得的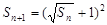 ,因为是正项数列,所以两边开方,得
,因为是正项数列,所以两边开方,得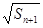 与
与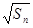 的地推关系式,从而判定数列形式,得出
的地推关系式,从而判定数列形式,得出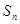 的通项公式,再根据
的通项公式,再根据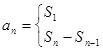
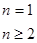 ,得出
,得出 的通项公式;(3)代入
的通项公式;(3)代入 的通项公式得到
的通项公式得到 ,然后裂项,经过裂项相消,得到
,然后裂项,经过裂项相消,得到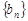 的前项和
的前项和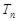 ,,通过分离常数可以判定
,,通过分离常数可以判定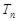 的单调性,求出最值,若
的单调性,求出最值,若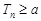 恒成立,那么
恒成立,那么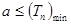 ,得到的范围.此题计算相对较大,属于中档题.
,得到的范围.此题计算相对较大,属于中档题.
试题解析:(1)解:因为点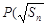 ,
,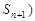 在曲线
在曲线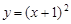 上,所以
上,所以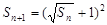 .
.
分别取 和
和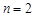 ,得到
,得到 ,
,
由 解得
解得 ,
,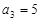 . 4分
. 4分
(2)解:由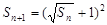 得
得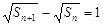 .
.
数列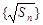 是以
是以 为首项,
为首项,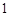 为公差的等差数列,所以
为公差的等差数列,所以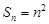 , 6分
, 6分
由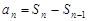
 ,当
,当 时,
时,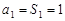 ,
,
所以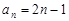 . 8分
. 8分
(3)解:因为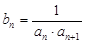

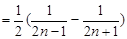 ,
,
所以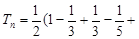

 , 11分
, 11分
显然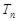 是关于
是关于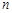 的增函数, 所以
的增函数, 所以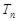 有最小值
有最小值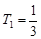 ,
,
因为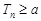 恒成立,所以
恒成立,所以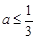 ,
,
因此 ,实数
,实数 的取值范围是
的取值范围是 ,
, . 13分
. 13分
考点:1.等差数列的定义;2.已知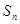 求
求 ;3.裂项相消;4.函数最值.
;3.裂项相消;4.函数最值.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. =
= ,求
,求 的值;
的值;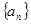 中,
中,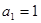 ,
,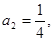 且
且
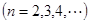 .
.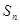 为数列
为数列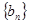 的前
的前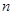 项和,且
项和,且
 .
. ,求数列
,求数列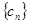 的前
的前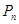 ;
;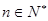 ,有
,有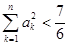 .
.
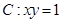 ,过
,过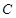 上一点
上一点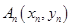 作一斜率为
作一斜率为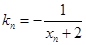 的直线交曲线
的直线交曲线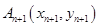 (
(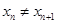 且
且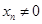 ,点列
,点列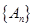 的横坐标构成数列
的横坐标构成数列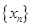 ,其中
,其中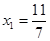 .
.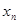 与
与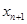 的关系式;
的关系式;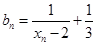 ,求证:数列
,求证:数列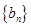 是等比数列;
是等比数列;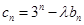 (
( 为非零整数,
为非零整数,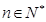 ),试确定
),试确定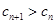 成立.
成立. 是等差数列,且
是等差数列,且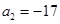 ,
,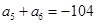 ;又若
;又若 是各项为正数的等比数列,且满足
是各项为正数的等比数列,且满足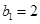 ,其前
,其前 项和为
项和为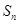 ,
,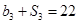 .
.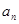 ,
,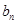 ;
;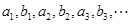 的前
的前 ,求
,求