题目内容
【题目】已知函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1 , x2(0<x1<x2<1)且满足f(x1)=f(x2),若k=5( ![]() +
+ ![]() ),且k为整数时,则k的值为( )(参考数据:e≈2.72)
),且k为整数时,则k的值为( )(参考数据:e≈2.72)
A.1
B.2
C.3
D.4
【答案】C
【解析】解:∵f(x)=xlnx,∴f′(x)=1+lnx,x>0, 由f′(x)=0,得x= ![]() ,
,
∵函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1 , x2(0<x1<x2<1)且满足f(x1)=f(x2),
∴x1lnx1=x2lnx2 ,
(0<x1< ![]() <x2<1),如图所示,
<x2<1),如图所示,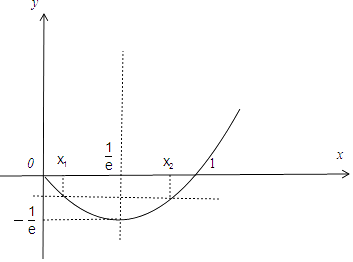
由 ![]() ,
, ![]() ,
,![]() <
< ![]() +
+ ![]() =
= ![]() ,
,
∵t= ![]() 关于x1单调递减,0<x1<
关于x1单调递减,0<x1< ![]() ,
,
∴ ![]() <
< ![]() ,∴5(
,∴5( ![]() +
+ ![]() )<
)< ![]() ,
,
∴k≤3.
∴k为整数时,则k的值为3.
故选:C.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

练习册系列答案
相关题目