题目内容
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
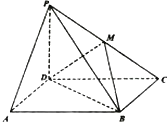
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
【答案】(1)详见解析;(2)详见解析.
【解析】
试题(1)设![]() ,由中位线定理证得
,由中位线定理证得![]() 平面
平面![]() ;(2)由
;(2)由![]() 平面
平面![]() 平面
平面![]() 平
平![]() .
.
试题解析:(1)设AC∩BD=H,连接MH,
∵H为平行四边形ABCD对角线的交点,∴H为AC中点,
又∵M为PC中点,∴MH为△PAC中位线,
可得MH∥PA,
MH平面MBD,PA平面MBD,
所以PA∥平面MBD.
(2)∵PD⊥平面ABCD,AD平面ABCD,
∴PD⊥AD,
又∵AD⊥PB,PD∩PB=D,
∴AD⊥平面PDB,结合BD平面PDB,得AD⊥BD
∵PD⊥BD,且PD、AD是平面PAD内的相交直线
∴BD⊥平面PAD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知定义在R上的函数y=f(x),满足f(2)=0,函数y=f(x+1)的图象关于点(-1,0)中心对称,且对任意的负数x1,x2(x1≠x2),![]() 恒成立,则不等式f(x)<0的解集为____.
恒成立,则不等式f(x)<0的解集为____.
【题目】为了研究“晚上喝绿茶与失眠”有无关系,调查了100名人士,得到下面的列联表:
失眠 | 不失眠 | 合计 | |
晚上喝绿茶 | 16 | 40 | 56 |
晚上不喝绿茶 | 5 | 39 | 44 |
合计 | 21 | 79 | 100 |
由已知数据可以求得:![]() ,则根据下面临界值表:
,则根据下面临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的结论是( )
A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”
B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”
C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”
D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”