题目内容
6.设f0(x)=|x-1|-10,fn(x)=|fn-1(x)|-(n+1)(n∈N*),则函数f20(x)的零点之和为2.分析 运用特殊函数f0(x)=|x-1|-10=$\left\{\begin{array}{l}{x-11,x≥10}\\{-9-x,x<1}\end{array}\right.$得出f1(x)的图象判断其零点的方法,再思考f20(x)=|f20(x)|-21,零点的位置,及个数,即可得出答案.
解答 解:∵f0(x)=|x-1|-10=$\left\{\begin{array}{l}{x-11,x≥10}\\{-9-x,x<1}\end{array}\right.$
∴f1(x)的图象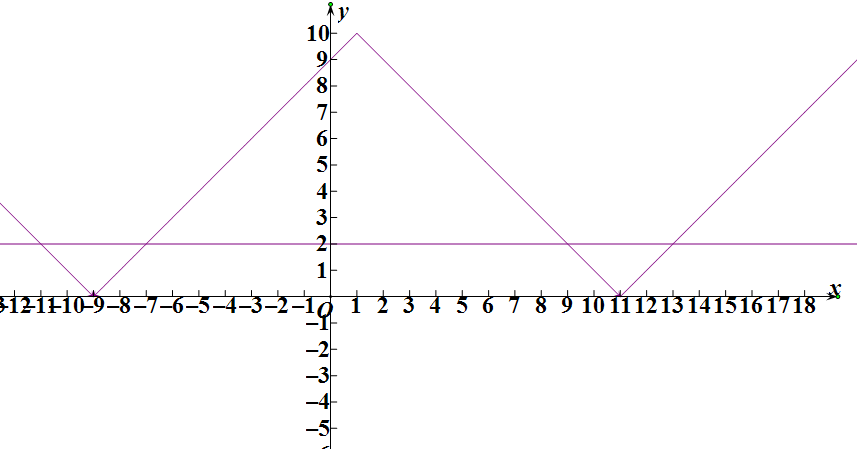
根据对称性得出零点的和为2×2=4,
f1(x)=|f0(x)|-2
根据对称性得出f1(x)的零点的和为2×2=4,
∵f20(x)=|f20(x)|-21,
∴图象关于x=1对称,利用折点的数据可得出只有2个零点,关于x=1对称,
∴函数f20(x)的零点之和为2
点评 本题考查了函数的零点问题,观察图象的能力,归纳能力,数学思维判断能力,属于中档题.

练习册系列答案
相关题目
1.满足A∪B={0,2}的集合A与B的组数为( )
| A. | 2 | B. | 5 | C. | 7 | D. | 9 |
18.在△ABC中,已知a4+b4+c4=2c2(a2+b2),则∠C=( )
| A. | 30° | B. | 60° | C. | 45°或135° | D. | 120° |
 如图,平面α,β,γ两两平行,且直线l与α,β,γ分别相交于点A,B,C,直线m与α,β,γ分别相交于点D,E,F,AB=6,BC=2,EF=3,求DE的长.
如图,平面α,β,γ两两平行,且直线l与α,β,γ分别相交于点A,B,C,直线m与α,β,γ分别相交于点D,E,F,AB=6,BC=2,EF=3,求DE的长. 如图所示,直角△ABC,∠B=90°,AB=1,BC=2,直线l⊥BC,若将△ABC绕直线l旋转一周,得到的几何体的体积是$\frac{8}{3}π$.
如图所示,直角△ABC,∠B=90°,AB=1,BC=2,直线l⊥BC,若将△ABC绕直线l旋转一周,得到的几何体的体积是$\frac{8}{3}π$.