题目内容
【题目】已知F1、F2分别为椭圆C： 
+ 
=1（a＞b＞0）的左、右焦点，且离心率为 
，点A（﹣ ， 
）在椭圆C上．
（1）求椭圆C的方程；
（2）是否存在斜率为k的直线l与椭圆C交于不同的两点M、N，使直线F2M与F2N的倾斜角互补，且直线l是否恒过定点，若存在，求出该定点的坐标；若不存在，说明理由．
【答案】
（1）解：∵F1、F2分别为椭圆C： 
+ 
=1（a＞b＞0）的左、右焦点，
且离心率为 
，点A（﹣ ， 
）在椭圆C上．
∴ 
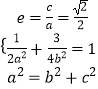，解得a2=2，b2=1．
∴椭圆C的方程为 
（2）解：由题意知直线MN存在斜率，其方程为y=kx+m，
由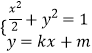 
，
消去y，得（2k2+1）x2+4kmx+2m2﹣2=0，
△=（4km）2﹣4（2k2+1）（2m2﹣2）＞0，
设M（ 
， 
，
又kF2M= 
， 
，
由已知直线F2M与F2N的倾斜角互补，
得 
．
化简，得2kx1x2+（m﹣k）（x1+x2）﹣2m=0，
∴ 
整理得m=﹣2k．
直线MN的方程为y=k（x﹣2），
因此直线MN过定点，该定点的坐标为（2，0）．
【解析】（1）由已知得 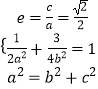，由此能求出椭圆C的方程．（2）由题意知直线MN存在斜率，其方程为y=kx+m，由 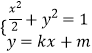，得（2k2+1）x2+4kmx+2m2﹣2=0，由此利用根的判别式和韦达定理结合已知条件推导出直线MN过定点（2，0）．
练习册系列答案
名校课堂系列答案
相关题目
