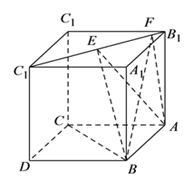题目内容
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 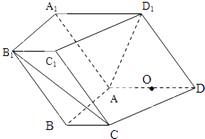
(1)求证:A1O∥平面AB1C;
(2)求锐二面角A﹣C1D1﹣C的余弦值.
【答案】
(1)证明:如图(1),

连接CO、A1O、AC、AB1,
则四边形ABCO为正方形,所以OC=AB=A1B1,
所以,四边形A1B1CO为平行四边形,
所以A1O∥B1C,
又A1O平面AB1C,B1C平面AB1C
所以A1O∥平面AB1C
(2)解:因为D1A=D1D,O为AD中点,所以D1O⊥AD
又侧面A1ADD1⊥底面ABCD,
所以D1O⊥底面ABCD,
以O为原点,OC、OD、OD1所在直线分别为x轴、y轴、z轴建立如图(2)所示的坐标系,

则C(1,0,0),D(0,1,0),D1(0,0,1),A(0,﹣1,0).所以 ![]() ,
,
设 ![]() 为平面C1CDD1的一个法向量,
为平面C1CDD1的一个法向量,
由 ![]() ,得
,得 ![]() ,
,
令z=1,则y=1,x=1,∴ ![]() .
.
又设 ![]() 为平面AC1D1的一个法向量,
为平面AC1D1的一个法向量,
由 ![]() ,得
,得 ![]() ,
,
令z1=1,则y1=﹣1,x1=﹣1,∴ ![]() ,
,
则 ![]() ,
,
故所求锐二面角A﹣C1D1﹣C的余弦值为 ![]()
【解析】(1)欲证A1O∥平面AB1C,根据直线与平面平行的判定定理可知只需证A1O与平面AB1C内一直线平行,连接CO、A1O、AC、AB1 , 利用平行四边形可证A1O∥B1C,又A1O平面AB1C,B1C平面AB1C,满足定理所需条件;(2)根据面面垂直的性质可知D1O⊥底面ABCD,以O为原点,OC、OD、OD1所在直线分别为x轴、y轴、z轴建立坐标系,求出平面C1CDD1的一个法向量 ![]() ,以及平面AC1D1的一个法向量
,以及平面AC1D1的一个法向量 ![]() ,然后求出两个法向量夹角的余弦值即可求出锐二面角A﹣C1D1﹣C的余弦值.
,然后求出两个法向量夹角的余弦值即可求出锐二面角A﹣C1D1﹣C的余弦值.

【题目】某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程 ![]() =bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
=bx+a中的b=﹣2,气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣销售量约为( )件.
A.46
B.40
C.38
D.58