题目内容
【题目】在正方体ABCD﹣A1B1C1D1中，E、F分别为CD、DD1的中点，则异面直线EF与A1C1所成角的余弦值为 ．
【答案】
【解析】解：取AD中点G，连结GF、GE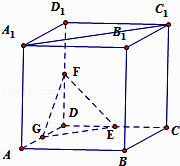 
由正方体的性质，可得EG∥A1C1 ， ∠GEF就是异面直线EF与A1C1所成角
设正方体的棱长等于2，可得
△GEF中，GE=GF=EF= 
∴∠GEF=60°，得cos∠GEF=
即异面直线EF与A1C1所成角的余弦值为
所以答案是：
【考点精析】认真审题，首先需要了解异面直线及其所成的角(异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系)．
练习册系列答案
相关题目
【题目】某商场为了了解毛衣的月销售量y（件）与月平均气温x（℃）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：
月平均气温x（℃） | 17 | 13 | 8 | 2 |
月销售量y（件） | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程 
=bx+a中的b=﹣2，气象部门预测下个月的平均气温约为6℃，据此估计该商场下个月毛衣销售量约为（ ）件．
A.46
B.40
C.38
D.58
【题目】连锁经营公司所属5个零售店某月的销售额利润资料如表：
商品名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
（参考公式： 
= 
= 
， 
= 
﹣ x）
（1）画出销售额和利润额的散点图
（2）若销售额和利润额具有相关关系，试计算利润额y对销售额x的回归直线方程．
（3）估计要达到1000万元的利润额，销售额约为多少万元．