题目内容
【题目】微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2. 
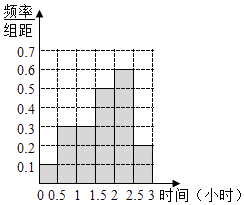
(1)确定x,y,p,q的值,并补全须率分布直方图;
(2)为进一步了解使用微信对自己的日不工作和生活是否有影响,从“微信达人”和“非微信达人”60人中用分层抽样的方法确定10人,若需从这10人中随积选取3人进行问卷调查,设选取的3人中“微信达人”的人数为X,求X的分布列和数学期望.
使用微信时间(单位:小时) | 频数 | 频率 |
(0,0.5] | 3 | 0.05 |
(0.5,1] | x | p |
(1,1.5] | 9 | 0.15 |
(1.5,2] | 15 | 0.25 |
(2,2.5] | 18 | 0.30 |
(2.5,3] | y | q |
合计 | 60 | 1.00 |
【答案】
(1)解:根据题意,有
 ,
,
解得x=9,y=6,
∴p=0.15,q=0.10,
补全频率分布图有右图所示
(2)解:用分层抽样的方法,从中选取10人,则其中“网购达人”有10× ![]() =4人,“非网购达人”有10×
=4人,“非网购达人”有10× ![]() =6人,
=6人,
∴ξ的可能取值为0,1,2,3,
P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =
= ![]() .
.
【解析】(1)根据分布直方图、频率分布表的性质,列出方程组,能确定x,y,p,q的值,并补全须率分布直方图.(2)用分层抽样的方法,从中选取10人,则其中“网购达人”有4人,“非网购达人”有6人,ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
【考点精析】本题主要考查了频率分布直方图和离散型随机变量及其分布列的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


