题目内容
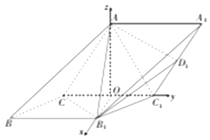
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2 ![]() .
. 
(1)求证:AB1⊥CC1;
(2)若AB1=3 ![]() ,A1C1的中点为D1 , 求二面角C﹣AB1﹣D1的余弦值.
,A1C1的中点为D1 , 求二面角C﹣AB1﹣D1的余弦值.
【答案】
(1)证明:连结AC1,则△ACC1,△B1C1C都是正三角形,
取CC1中点O,连结OA,OB1,
则CC1⊥OA,CC1⊥OB1,
∵OA∩OB1=O,∴CC1⊥平面OAB1,
∵AB1平面OAB1,∴CC1⊥AB1
(2)解:由(1)知OA=OB1=3,
又AB1=3 ![]() ,∴OA2+OB12=AB12,
,∴OA2+OB12=AB12,
∴OA⊥OB1,OA⊥平面B1C1C,
如图,分别以OB1,OC1,OA为x,y,z轴,建立空间直角坐标系,
则C(0,﹣ ![]() ,0),B1(3,0,0),A(0,0,3),C1(0,
,0),B1(3,0,0),A(0,0,3),C1(0, ![]() ,0),A1(0,2
,0),A1(0,2 ![]() ,3),D1(0,
,3),D1(0, ![]() ,
, ![]() ),
),
设平面CAB1的法向量 ![]() =(x,y,z),
=(x,y,z),
∵ ![]() =(3,0,﹣3),
=(3,0,﹣3), ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
∴ 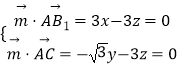 ,取x=1,得
,取x=1,得 ![]() =(
=( ![]() ),
),
设平面AB1D1的法向量 ![]() =(a,b,c),
=(a,b,c),
∵ ![]() =(0,
=(0, ![]() ,﹣
,﹣ ![]() ),
), ![]() =(﹣3,
=(﹣3, ![]() ,
, ![]() ),
),
∴  ,取b=1,得
,取b=1,得 ![]() =(
=( ![]() ),
),
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
由图知二面角C﹣AB1﹣D1的平面角为钝角,
∴二面角C﹣AB1﹣D1的余弦值为﹣ ![]() .
.
【解析】(1)连结AC1 , 则△ACC1 , △B1C1C都是正三角形,取CC1中点O,连结OA,OB1 , 则CC1⊥OA,CC1⊥OB1 , 由此能证明CC1⊥AB1 . (2)分别以OB1 , OC1 , OA为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣AB1﹣D1的余弦值.
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】微信是现代生活进行信息交流的重要工具,随机对使用微信的60人进行了统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信达人”,不超过2两小时的人被定义为“非微信达人”,己知“非微信达人”与“微信达人”人数比恰为3:2. 
(1)确定x,y,p,q的值,并补全须率分布直方图;
(2)为进一步了解使用微信对自己的日不工作和生活是否有影响,从“微信达人”和“非微信达人”60人中用分层抽样的方法确定10人,若需从这10人中随积选取3人进行问卷调查,设选取的3人中“微信达人”的人数为X,求X的分布列和数学期望.
使用微信时间(单位:小时) | 频数 | 频率 |
(0,0.5] | 3 | 0.05 |
(0.5,1] | x | p |
(1,1.5] | 9 | 0.15 |
(1.5,2] | 15 | 0.25 |
(2,2.5] | 18 | 0.30 |
(2.5,3] | y | q |
合计 | 60 | 1.00 |
【题目】某品牌的汽车4S店,对最近100例分期付款购车情况进行统计,统计结果如表所示,已知分9期付款的频率为0.4;该店经销一辆该品牌的汽车.若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 | a | b |
(1)若以表中计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3位顾客,求事件A:“至多有1位采用分6期付款”的概率P(A);
(2)按分层抽样的方式从这100位顾客中抽出5人,再从抽出的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量η,求η的分布列及数学期望E(η).

