题目内容
设等差数列{an}的前n项和为Sn,且Sn=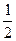 nan+an—c(c是常数,n∈N*),a2=6.
nan+an—c(c是常数,n∈N*),a2=6.
(Ⅰ)求c的值及{an}的通项公式;
(Ⅱ)证明: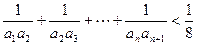
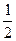 nan+an—c(c是常数,n∈N*),a2=6.
nan+an—c(c是常数,n∈N*),a2=6.(Ⅰ)求c的值及{an}的通项公式;
(Ⅱ)证明:
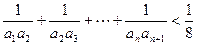
(Ⅰ) c=2;an=2n+2
(Ⅱ)证明见解析。
(Ⅱ)证明见解析。
(Ⅰ)解:因为Sn=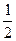 nan+an—c,
nan+an—c,
所以当n=1时,S1=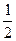 a1+a1—c,解得a1=2c, …… 2分
a1+a1—c,解得a1=2c, …… 2分
当n=2时,S2=a2+a2—c,即a1+a2=2a2—c,解得a2=3c,
所以3c=6,解得c=2; ……4分
则a1=4,数列{an}的公差d=a2—a1=2,
所以an=al+(n—1)d=2n+2. …… 6分
(Ⅱ);因为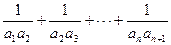
=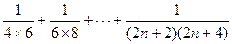 ……7分
……7分
=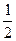 (
(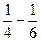 )+
)+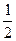 (
(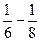 )+…+
)+…+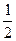 (
( ……8分
……8分
=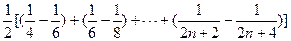
=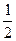 (
(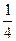
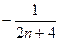 )
)
=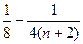 . …… 10分
. …… 10分
因为n∈N*, 所以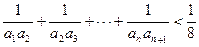 . ……12分
. ……12分
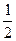 nan+an—c,
nan+an—c,所以当n=1时,S1=
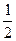 a1+a1—c,解得a1=2c, …… 2分
a1+a1—c,解得a1=2c, …… 2分当n=2时,S2=a2+a2—c,即a1+a2=2a2—c,解得a2=3c,
所以3c=6,解得c=2; ……4分
则a1=4,数列{an}的公差d=a2—a1=2,
所以an=al+(n—1)d=2n+2. …… 6分
(Ⅱ);因为
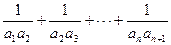
=
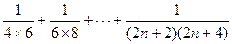 ……7分
……7分=
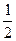 (
(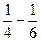 )+
)+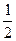 (
(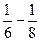 )+…+
)+…+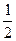 (
( ……8分
……8分=
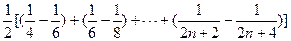
=
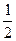 (
(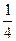
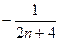 )
)=
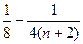 . …… 10分
. …… 10分因为n∈N*, 所以
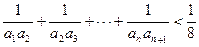 . ……12分
. ……12分
练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
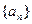 满足:
满足: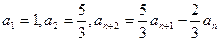 ,(n=1,2,…)。
,(n=1,2,…)。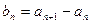 ,(n=1,2,…)。求数列
,(n=1,2,…)。求数列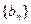 的通项公式;(2)求数列
的通项公式;(2)求数列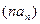 的前n项和Sn。
的前n项和Sn。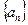 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈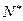 .
.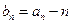 ,求数列
,求数列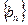 的通项公式;
的通项公式;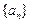 满足:
满足: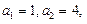 且对任意的
且对任意的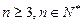 有
有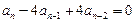 .
.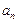 ;
;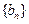 ,使得对任意的
,使得对任意的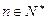 有
有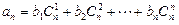 成立?证明你的结论
成立?证明你的结论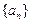 满足:
满足: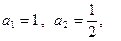 且
且 .
.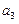 ,
,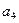 ,
,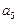 ,
,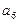 的值及数列
的值及数列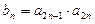 ,求数列
,求数列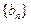 的前
的前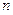 项和
项和 ;
;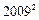
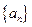 为等差数列,首项
为等差数列,首项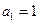 ,公差
,公差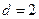 ,
,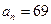 ,则
,则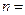 ( )
( )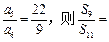 ______________.
______________.