题目内容
已知数列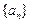 满足:
满足: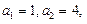 且对任意的
且对任意的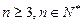 有
有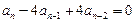 .
.
(Ⅰ)求数列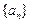 的通项公式
的通项公式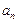 ;
;
(Ⅱ)是否存在等差数列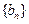 ,使得对任意的
,使得对任意的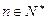 有
有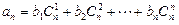 成立?证明你的结论
成立?证明你的结论
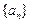 满足:
满足: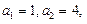 且对任意的
且对任意的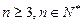 有
有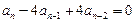 .
.(Ⅰ)求数列
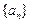 的通项公式
的通项公式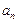 ;
;(Ⅱ)是否存在等差数列
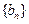 ,使得对任意的
,使得对任意的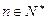 有
有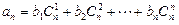 成立?证明你的结论
成立?证明你的结论(Ⅰ)

(Ⅱ)
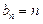 ,即
,即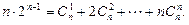
(Ⅰ)解:∵
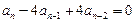
∴

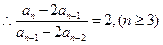
∴数列
 是首项为(
是首项为( ),公比为2的等比数列,………………4分
),公比为2的等比数列,………………4分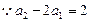 ,
,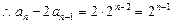

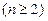
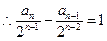 ,∴数列
,∴数列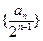 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列 ,∴
,∴ … …………………7分
… …………………7分(Ⅱ)令
 代入
代入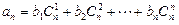 得:
得: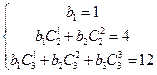 解得:
解得: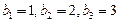
由此可猜想
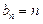 ,即
,即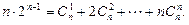 …………………10分
…………………10分下面用数学归纳法证明:
(1)当n=1时,等式左边=1,右边=
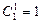 ,
,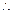 当n=1时,等式成立,
当n=1时,等式成立,(2)假设当n=k时,等式成立,即
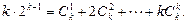
当n=k+1时
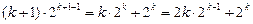

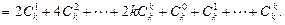
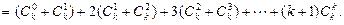
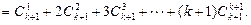
∴当n=k+1时,等式成立,
综上所述,存在等差数列
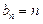 ,使得对任意的
,使得对任意的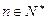 有
有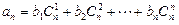 成立。 …………………14分
成立。 …………………14分
练习册系列答案
相关题目
 ,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设
,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设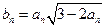 ,证明bn<bn+1,其中n为正整数.
,证明bn<bn+1,其中n为正整数.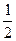 nan+an—c(c是常数,n∈N*),a2=6.
nan+an—c(c是常数,n∈N*),a2=6.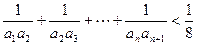
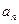 }的前n项和满足
}的前n项和满足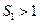 ,且
,且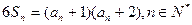
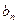 }满足
}满足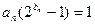 ,并记
,并记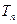 为{
为{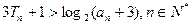 . (7分)
. (7分)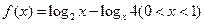 ,数列
,数列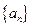 的通项
的通项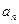 满足
满足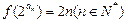 .
. ,且与直线
,且与直线 相切,动圆圆心Q的轨迹为曲线C,过定点
相切,动圆圆心Q的轨迹为曲线C,过定点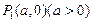 作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点
作与y轴平行的直线且和曲线C相交于点M1,然后过点M1作C的切线和x轴交于点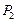 ,再过
,再过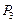 ,如此继续下去直至无穷,记△
,如此继续下去直至无穷,记△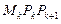 的面积为
的面积为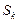
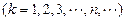

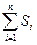 的值。
的值。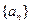 的前
的前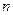 项和为
项和为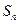 ,已知
,已知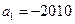 ,
,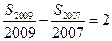 ,则
,则 ()
() 的前
的前 项和记作
项和记作 ,满足
,满足 ,
, .
. 求出数列
求出数列 ,且
,且 对正整数
对正整数 的范围;
的范围; 证明:
证明: 中不可能有等差子数列(已知
中不可能有等差子数列(已知 。
。