题目内容
19.若f(x)是R上周期为5的奇函数,且满足f(-2)=2,则f(2012)-f(2010)=( )| A. | 2 | B. | -2 | C. | 0 | D. | -4 |
分析 根据函数的周期性和奇偶性的关系进行转化即可.
解答 解:∵函数f(x)是周期为5的周期函数,
∴f(2012)=f(2010+2)=f(2),f(2010)=f(0),
∵f(x)是奇函数,且满足f(-2)=2,
∴f(0)=0,f(2)=-2,
则f(2012)-f(2010)=f(2)-f(0)=-2-0=-2,
故选:B
点评 本题主要考查函数值是计算,根据函数奇偶性和周期性进行转化是解决本题的关键.

练习册系列答案
相关题目
10.焦点在x轴上的椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4+k}$=1的离心率为$\frac{4}{5}$,则k的值为( )
| A. | 21 | B. | $-\frac{181}{25}$ | C. | -$\frac{19}{25}$ | D. | $\frac{19}{25}$ |
7.P为椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1上任意一点,EF为圆N:(x-1)2+y2=4的任意一条直径,则$\overrightarrow{PE}$•$\overrightarrow{PF}$的取值范围是( )
| A. | [0,15] | B. | [5,15] | C. | [5,21] | D. | (5,21) |
11.若复数z=i3+$\frac{1}{1+i}$(i为虚数单位),则复数z的模为( )
| A. | 2$\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
9.在等差数列{an}中,Sn是其前n项和,a1=-2010,$\frac{{{S_{2008}}}}{2008}-\frac{{{S_{2006}}}}{2006}$=2,则S2010=( )
| A. | -2009 | B. | 2009 | C. | -2010 | D. | 2010 |
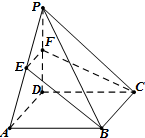 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点E,F为PA,PD的中点,则面BCFE将四棱锥P-ABCD所分成的上下两部分的体积的比值为$\frac{3}{5}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点E,F为PA,PD的中点,则面BCFE将四棱锥P-ABCD所分成的上下两部分的体积的比值为$\frac{3}{5}$.