题目内容

4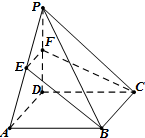．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，点E，F为PA，PD的中点，则面BCFE将四棱锥P-ABCD所分成的上下两部分的体积的比值为$\frac{3}{5}$．

分析 不妨设ABCD是正方形，PD⊥平面ABCD，AD=2a，求出上下两部分的体积，即可得出结论．

解答 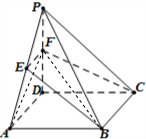解：不妨设ABCD是正方形，PD⊥平面ABCD，AD=2a，则
VP-ABCD=$\frac{1}{3}×2a×2a×2a$=$\frac{8}{3}$a3，
连接FA，FB，则VEFABCD=$\frac{1}{2}×\frac{8}{3}{a}^{3}$+$\frac{1}{3}×\frac{1}{2}×a×a×2a$=$\frac{5}{3}$a3，
∴VP-EFBC=a3，
∴四棱锥P-ABCD所分成的上下两部分的体积的比值为$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．

点评 本题考查体积的计算，考查学生的计算能力，正确计算体积是关键．

练习册系列答案
相关题目
6．根据下列条件，求x的值：
（1）4×4x-5×2x-6=0；
（2）9x+6x=22x+1．
15．已知x＞0，y＞0，且2x+9y=1，则$\frac{1}{x}$+$\frac{x}{y}$的最小值为（　　）
A．6B．8C．$\frac{17}{2}$D．11+6$\sqrt{2}$
12．已知在直角坐标系xOy中，直线l的参数方程是$\left\{\begin{array}{l}{x=2+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数），在极
坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的极坐标方程为ρ=4$\sqrt{2}$cos（θ+$\frac{π}{4}$）．
（Ⅰ）将圆C的极坐标方程化为直角坐标方程；
（Ⅱ）若直线l与圆C相交于A，B两点，点P的坐标为（2，0），试求$\frac{1}{|PA|}$+$\frac{1}{|PB|}$的值．
19．若f（x）是R上周期为5的奇函数，且满足f（-2）=2，则f（2012）-f（2010）=（　　）
A．2B．-2C．0D．-4
9．设集合U=R，M={x||x|＜2}，N={y|y=2x-1}，则M∩（∁UN）=（　　）
A．[-1，2）B．（-2，2）C．（-2，+∞）D．（-2，-1]
16．若tanα＞0，则sin2α的符号是正号．（填“正号”、“负号”或“符号不确定”）
13．某几何体的三视图如图所示，则该几何体的体积是（　　）
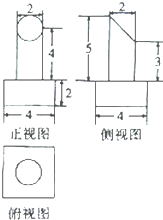
A．8+4πB．32+$\frac{11}{3}$πC．16+16πD．32+4π
14．数列{an}满足a1=2，${a_{n+1}}=\frac{a_n}{{1+3{a_n}}}$，令${b_n}=\frac{1}{a_n}$
（Ⅰ）求证：{bn}为等差数列；         
（Ⅱ）求{an}的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网