题目内容
17.由曲线y=x2和直线x=0,x=2,y=t2,t∈[0,2]围成的封闭图形的面积记为S.(1)用t表示S.
(2)求S的最大值和最小值.
分析 (1)由图形将阴影部分的面积用定积分表示出来,再利用定积分的运算规则将面积表示为t的函数;
(2)求导数,确定函数的单调性,即可求S的最大值和最小值.
解答 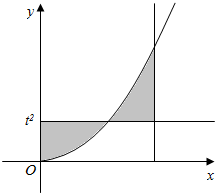 解:(1)由题意及图象,曲线y=x2和直线y=t2交点坐标是(t,t2)
解:(1)由题意及图象,曲线y=x2和直线y=t2交点坐标是(t,t2)
故阴影部分的面积是∫0t(t2-x2)dx+∫t2(-t2+x2)dx=(t2x-$\frac{1}{3}$x3)|0t+(-t2x+$\frac{1}{3}$x3)|t2=$\frac{4}{3}{t}^{3}-2{t}^{2}+\frac{8}{3}$;
(2)令p=$\frac{4}{3}{t}^{3}-2{t}^{2}+\frac{8}{3}$,则p′=4t2-4t=4t(t-1),
知p=$\frac{4}{3}{t}^{3}-2{t}^{2}+\frac{8}{3}$在[0,1]上是减函数,在[1,2]上是增函数,
∴在t=1时取到最小值,面积的最小值是2;t=0时,面积最大,最大值为$\frac{8}{3}$.
点评 本题考查求定积分,解题的关键是根据图象与函数解析式将面积用积分表示出来,利用积分的定义得到关于变量t的表达式,再研究其单调性求出最值,本题运算量较大涉及到的考点较多,综合性强,运算量大,极易因运算、变形出错.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
8.下列四个选项中错误的是( )
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0则x=1”. | |
| B. | 若p∧q为真命题,则p∨q为真命题. | |
| C. | 若命题p:?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0. | |
| D. | “x>2”是“x2-3x+2>0”成立的必要不充分条件. |
5.如果函数f(x)=(a2-2)x在R上是减函数,那么实数a的取值范围是( )
| A. | |a|>$\sqrt{2}$ | B. | $\sqrt{2}$<|a|<$\sqrt{3}$ | C. | |a|>$\sqrt{3}$ | D. | |a|<3 |
 △ABC中D是BC边上的一个四等分点,AE:EF:FC=2;2:3,已知△DEF的面积为12cm2,那么△ABC的面积是多少?
△ABC中D是BC边上的一个四等分点,AE:EF:FC=2;2:3,已知△DEF的面积为12cm2,那么△ABC的面积是多少?