题目内容
椭圆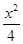 +
+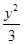 =1的右焦点到直线y=
=1的右焦点到直线y=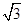 x的距离是 ( )
x的距离是 ( )
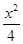 +
+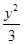 =1的右焦点到直线y=
=1的右焦点到直线y=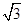 x的距离是 ( )
x的距离是 ( )A.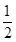 | B.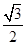 | C.1 | D.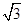 |
B
试题分析:由于椭圆
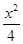 +
+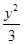 =1的几何性质可知a=2,b=
=1的几何性质可知a=2,b=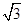 ,结合a,b,c的关系式
,结合a,b,c的关系式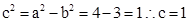 ,那么焦点的位置根据方程中4>3,说明焦点在x轴上,且为(1,0),而直线方程y=
,那么焦点的位置根据方程中4>3,说明焦点在x轴上,且为(1,0),而直线方程y=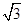 x的化为的一般式为
x的化为的一般式为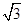 x—y=0的,代入点到直线的距离公式中
x—y=0的,代入点到直线的距离公式中 ,故可知选B.
,故可知选B.点评:解决该试题的关键是通过已知条件得到椭圆的有焦点,代入点到直线的距离公式中求解即可。易错点就是a,b,c的平方关系的准确运用。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
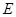 :
: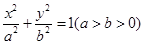 的左焦点为
的左焦点为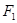 ,右焦点为
,右焦点为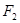 ,离心率
,离心率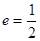 .过
.过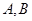 两点,且△
两点,且△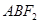 的周长为
的周长为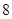 .
.
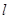 :
: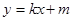 与椭圆
与椭圆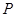 ,且与直线
,且与直线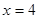 相交于点
相交于点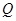 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点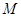 ,使得以
,使得以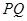 为直径的圆恒过点
为直径的圆恒过点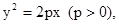 过焦点
过焦点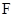 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;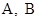 两点, 存在定点
两点, 存在定点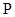 , 使得
, 使得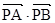 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.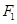 ,
, 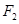 是椭圆
是椭圆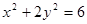 的两个焦点,点
的两个焦点,点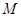 在此椭圆上且
在此椭圆上且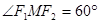 ,则
,则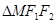 的面积等于( )
的面积等于( )
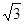

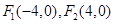 ,动点
,动点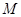 满足条件:
满足条件: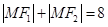 ,则点
,则点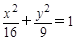
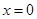
 (
(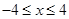 )
)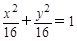
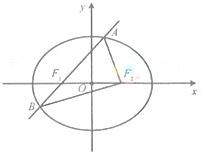
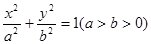 的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )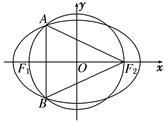


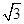 -1
-1 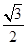
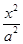 +
+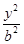 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,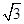 ,
,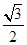 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.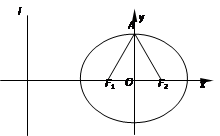




 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 ,最小值为
,最小值为 .
. 与椭圆
与椭圆 ,
, 两点(
两点(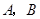 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.