题目内容
4.已知f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2ax+$\frac{1}{x}$(a为实数).(1)当x∈(0,1]时,求f(x)的解析式;
(2)若0<a<$\frac{1}{a}$时,判断f(x)在x∈(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最小值6.
分析 (1)当x∈(0,1]时,-x∈[-1,0),将-x代入函数的解析式结合函数的奇偶性求出即可;
(2)通过讨论a的范围,根据函数的单调性的定义证明即可;
(3)假设存在,利用基本不等式的性质求出即可.
解答 解:(1)∵函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,
当x∈[-1,0)时,f(x)=2ax+$\frac{1}{x}$(a为实数).
∴当x∈(0,1]时,-x∈[-1,0)
∴f(-x)=-2ax-$\frac{1}{x}$=-f(x),
∴f(x)=2ax+$\frac{1}{x}$;
(2)由(1)得:x∈(0,1]时:f(x)=2ax+$\frac{1}{x}$,
设0<x1<x2≤1,
则f(x1)-f(x2)=2ax1+$\frac{1}{{x}_{1}}$-2ax2-$\frac{1}{{x}_{2}}$=$\frac{{(x}_{1}{-x}_{2})(2a-1)}{{x}_{1}{•x}_{2}}$,
$\frac{1}{2}$<a<1时:2a-1>0,x1-x2<0,f(x1)<f(x2),
函数f(x)在(0,1]递增;
0<a≤$\frac{1}{2}$时:2a-1<0,x1-x2<0,f(x1)>f(x2),
函数f(x)在(0,1]递减;
(3)假设存在实数a,使得当x∈(0,1]时,f(x)有最小值6,则a>0,
∴f(x)=2ax+$\frac{1}{x}$≥2$\sqrt{2ax•\frac{1}{x}}$=2$\sqrt{2a}$=6,解得:a=$\frac{9}{2}$,当且仅当x=$\sqrt{\frac{1}{2a}}$=$\frac{1}{3}$时“=”成立.
点评 本题考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想,是高考的重点,解题时要认真审题,注意函数性质的灵活运用.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{5}{2}$-$\frac{2n+5}{{2}^{n+1}}$ | B. | 5-$\frac{2n+5}{{2}^{n}}$ | C. | $\frac{2n+1}{{2}^{n}}+1$ | D. | $\frac{2n+5}{{2}^{n}}$-1 |
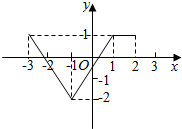 根据如图所示的函数y=f(x)的图象,写出函数的解析式.
根据如图所示的函数y=f(x)的图象,写出函数的解析式.