题目内容
15.已知函数y=-x2+x-6,若使图象都在x轴的下方,求x的取值范围.分析 根据已知中函数的解析式,分析函数图象的形状,进而可得答案.
解答 解:∵△=1-24<0,
∴函数y=-x2+x-6的图象开口方向朝下,且与x轴没有交点,
此时函数图象恒在x轴下方,
故满足条件的x的取值范围为R.
点评 本题考查的知识点是二次函数,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知函数f(x)=sin(2x-$\frac{π}{6}$),则下面说法正确的是( )
| A. | 函数图象关于点($\frac{π}{12}$,0)对称 | B. | 函数图象的-条对称轴方程为x=$\frac{π}{6}$ | ||
| C. | 函数f(x)是奇函数 | D. | 函数f(x)是偶函数 |
7.若数列{an}的通项公式为an=$\frac{1}{3}$(10n-1),则{an}的前n项和为( )
| A. | $\frac{1{0}^{n+1}-10}{27}$-$\frac{n}{3}$ | B. | $\frac{1{0}^{n}-1}{9}$-$\frac{n}{3}$ | C. | $\frac{1{0}^{n}-n-1}{9}$ | D. | $\frac{1{0}^{n}}{9}$ |
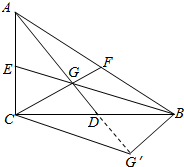 如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.
如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.