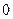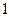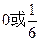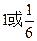题目内容
对于三次函数
 。
。
定义:(1)设 是函数
是函数 的导数
的导数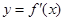 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;
定义:(2)设 为常数,若定义在
为常数,若定义在 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)

 。
。定义:(1)设
 是函数
是函数 的导数
的导数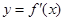 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;定义:(2)设
 为常数,若定义在
为常数,若定义在 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。己知
 ,请回答下列问题:
,请回答下列问题:(1)求函数
 的“拐点”
的“拐点”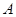 的坐标
的坐标(2)检验函数
 的图象是否关于“拐点”
的图象是否关于“拐点”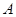 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)(3)写出一个三次函数
 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)(1)“拐点”坐标是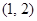 ;
;
(2)一般地,三次函数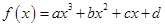
 的“拐点”是
的“拐点”是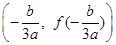 ,它就是
,它就是 的对称中心。
的对称中心。
或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数.
(3)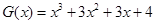 或
或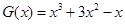 .
.
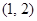 ;
;(2)一般地,三次函数
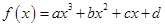
 的“拐点”是
的“拐点”是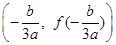 ,它就是
,它就是 的对称中心。
的对称中心。或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数.
(3)
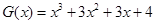 或
或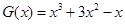 .
.试题分析:(1)依题意,计算
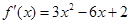 ,
,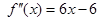 .
.由
 ,得
,得 ,再据
,再据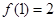 ,可得“拐点”坐标是
,可得“拐点”坐标是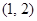 .
.(2)由(1)知“拐点”坐标是
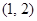 .
.根据定义(2),考查
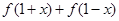
=

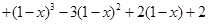
=
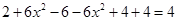 =
=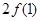 ,
,作出结论:
一般地,三次函数
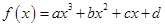
 的“拐点”是
的“拐点”是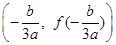 ,它就是
,它就是 的对称中心.
的对称中心.或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数.
(3)根据(2)写出
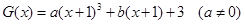 或写出一个具体的函数,如
或写出一个具体的函数,如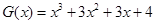 或
或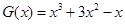 .
.试题解析:(1)依题意,得:
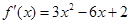 ,
, 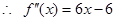 。 2分
。 2分由
 ,即
,即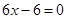 。∴
。∴ ,又
,又 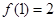 ,
,∴
 的“拐点”坐标是
的“拐点”坐标是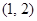 .。 4分
.。 4分 (2)由(1)知“拐点”坐标是
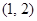 .
.而
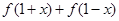 =
=
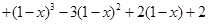
=
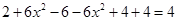 =
=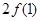 ,
,由定义(2)知:
 关于点
关于点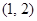 对称。 8分
对称。 8分一般地,三次函数
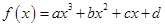
 的“拐点”是
的“拐点”是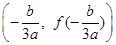 ,它就是
,它就是 的对称中心. 10分
的对称中心. 10分(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数 )都可以给分
(3)
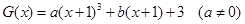 或写出一个具体的函数,如
或写出一个具体的函数,如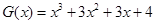 或
或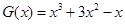 . 12分
. 12分
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
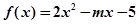 的导函数为
的导函数为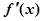 ,若
,若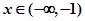 时,
时,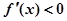 ;
;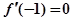 ;
;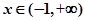 时,
时,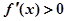 ,则
,则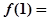 ( )
( )
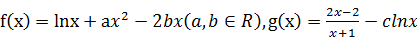 .
.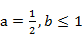 时,
时,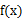 与
与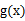 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 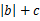 的最小值。
的最小值。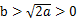 时,求证:存在
时,求证:存在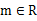 ,使
,使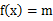 的三个不同的实数解
的三个不同的实数解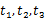 ,且对任意
,且对任意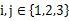 且
且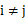 都有
都有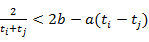 .
. 上的函数
上的函数 ,
,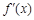 是它的导函数,且恒有
是它的导函数,且恒有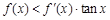 成立,则( )
成立,则( )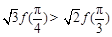
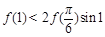
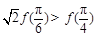
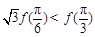
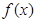 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为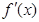 ,且有
,且有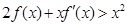 ,则不等式
,则不等式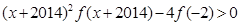 的解集为( )
的解集为( )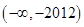
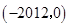

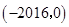
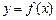 的图像在点M
的图像在点M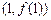 处的切线方程是
处的切线方程是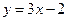 ,
, = 。
= 。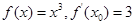 ,则
,则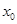 的值为____ .
的值为____ . 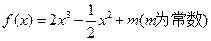 图象上
图象上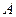 处的切线与
处的切线与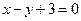 的夹角为
的夹角为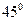 ,则
,则