题目内容
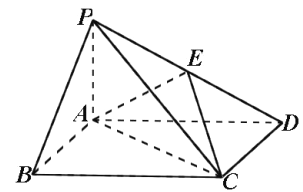
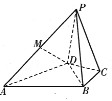
【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)利用中位线关系,得出![]() //
//![]() ,然后再根据题意证明
,然后再根据题意证明![]() //
//![]() ,即可得出结论
,即可得出结论
(2)先证明出![]() 平面
平面![]() ,然后以
,然后以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,然后计算出平面
轴建立如图所示的空间直角坐标系,然后计算出平面![]() 的法向量
的法向量![]() 和
和![]() ,最后,利用公式求解
,最后,利用公式求解![]() 求解即可
求解即可
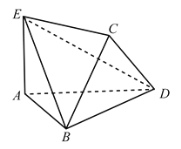
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() //
//![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
又![]() ,所以
,所以![]() //
//![]() .
.
又![]() ,
,![]() ,
,
所以平面![]() //平面
//平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
(2)连接![]() ,
,![]() ,
,
则![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.
又![]() ,
,![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
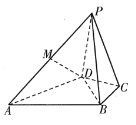
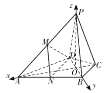
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,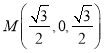 ,
,
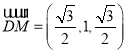 ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
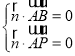 则
则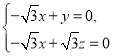 得
得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
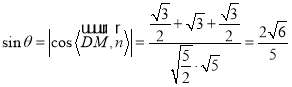 .
.
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】阿尔法狗(AlphaGo)是第一个击败人类职业围棋选手、第一个战胜围棋世界冠军的人工智能程序,由谷歌(Google)公司的团队开发.其主要工作原理是“深度学习”.2017 年5 月,在中国乌镇围棋峰会上,它与排名世界第一的世界围棋冠军柯洁对战,以3 比0 的总比分获胜.围棋界公认阿尔法围棋的棋力已经超过人类职业围棋顶尖水平.
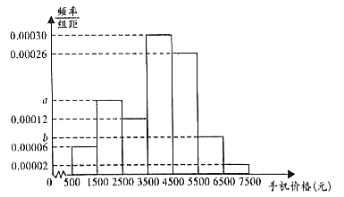
为了激发广大中学生对人工智能的兴趣,某市教育局组织了一次全市中学生“人工智能”软件设计竞赛,从参加比赛的学生中随机抽取了30 名学生,并把他们的比赛成绩按五个等级进行了统计,得到如下数据表:
成绩等级 |
|
|
|
|
|
成绩(分) | 5 | 4 | 3 | 2 | 1 |
人数(名) | 4 | 6 | 10 | 7 | 3 |
(1)根据上面的统计数据,试估计从本市参加比赛的学生中任意抽取一人,其成绩等级为“![]() 或
或![]() ”的
”的
概率;
(2)根据(I)的结论,若从该地区参加比赛的学生(参赛人数很多)中任选3 人,记![]() 表示抽到成绩等级为“
表示抽到成绩等级为“![]() 或
或![]() ”的学生人数,求
”的学生人数,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() ;
;
(3)从这30 名学生中,随机选取2 人,求“这两个人的成绩之差大于1分”的概率.