题目内容
【题目】已知曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)化![]() 、
、![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,求
,求![]() 的中点
的中点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1) ![]() :
:![]() ;
;![]() :
:![]() ;
;![]() 以圆心为
以圆心为![]() ,半径为1的圆,
,半径为1的圆,![]() 以坐标原点为中心,焦点在
以坐标原点为中心,焦点在![]() 轴的椭圆;(2)
轴的椭圆;(2)![]()
【解析】
(1)直接利用参数方程组消去参数即可得到它们的普通方程;
(2)根据已知条件分别求出![]() 、
、![]() 两点坐标以及
两点坐标以及![]() 点坐标,再利用点到直线的距离公式即可求出.
点坐标,再利用点到直线的距离公式即可求出.
(1)曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),
即![]() ,且
,且![]() ,则
,则
![]() :
:![]() ;
;
![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),
即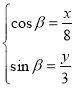 ,且
,且![]() ,则
,则
![]() :
:![]() ;
;
![]() 以圆心为
以圆心为![]() ,半径为1的圆,
,半径为1的圆,
![]() 以坐标原点为中心,焦点在
以坐标原点为中心,焦点在![]() 轴的椭圆;
轴的椭圆;
(2)曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,
,
所以![]() ,
,
曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,
,
所以![]() ,
,
所以![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
因为直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,
,
即直线![]() 的普通方程为:
的普通方程为:![]() ,
,
所以![]() 的中点
的中点![]() 到直线
到直线![]() 的距离
的距离![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某语文报社为研究学生课外阅读时间与语文考试中的作文分数的关系,随机调查了本市某中学高三文科班![]() 名学生每周课外阅读时间
名学生每周课外阅读时间![]() (单位:小时)与高三下学期期末考试中语文作文分数
(单位:小时)与高三下学期期末考试中语文作文分数![]() ,数据如下表:
,数据如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 38 | 40 | 43 | 45 | 50 | 54 |
(1)根据上述数据,求出高三学生语文作文分数![]() 与该学生每周课外阅读时间
与该学生每周课外阅读时间![]() 的线性回归方程,并预测某学生每周课外阅读时间为
的线性回归方程,并预测某学生每周课外阅读时间为![]() 小时时其语文作文成绩;
小时时其语文作文成绩;
(2)从这![]() 人中任选
人中任选![]() 人,这
人,这![]() 人中至少有
人中至少有![]() 人课外阅读时间不低于
人课外阅读时间不低于![]() 小时的概率.
小时的概率.
参考公式:![]() ,其中
,其中 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]()