题目内容
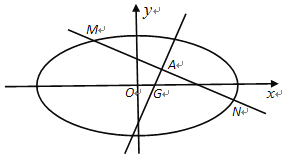
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
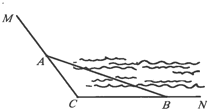
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
【答案】(1)10;(2)8![]() .
.
【解析】
(1)利用a、b、c成等差数列,且公差为4,可得![]() ,利用余弦定理即可求b的值;
,利用余弦定理即可求b的值;
(2)利用正弦定理,求出AC、BC,可得到观景路线A-C-B为![]() 是关于
是关于![]() 的函数,求出最大值即可
的函数,求出最大值即可
解:(1)∵a、b、c成等差数列,且公差为4,∴![]() ,
,
∵∠MCN=120°,
∴![]() ,即
,即![]() °,
°,
∴b=10
(2)由题意,在![]() 中,
中,![]() ,
,
则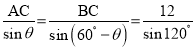 ,
,
∴![]() ,
,![]() ,
,
∴观景路线A-C-B的长![]() ,且
,且![]() ,
,
∴θ=30°时,观景路线A-C-B长的最大值为8![]()

练习册系列答案
相关题目