题目内容
【题目】某学校为调查该校学生每周使用手机上网的时间，随机收集了若干位学生每周使用手机上网的时间的样本数据（单位：小时），将样本数据分组为
，绘制了如下图所示的频率分布直方图，已知
内的学生有5人．
（1）求样本容量
，并估计该校学生每周平均使用手机上网的时间；
（2）将使用手机上网的时间在
内定义为“长时间看手机”；使用手机上网的时间在
内定义为“不长时间看手机”．已知在样本中有
位学生不近视，其中“不长时间看手机”的有
位学生．请将下面的
列联表补充完整，并判断能否在犯错误的概率不超过
的前提下认为该校学生长时间看手机与近视有关．
近视 | 不近视 | 合计 | |
长时间看手机 | |||
不长时间看手机 | 15 | ||
合计 | 25 |
参考公式和数据：
．
|
|
|
|
|
|
|
|
|
|
|
|
【答案】（1）5.8；（2）见解析
【解析】
（1）因为使用手机上网的时间在
内的有5人，对应的频率为
，
所以样本容量
，
由题可得该校学生每周平均使用手机上网的时间约为
小时．
（2）由题可得样本中“不长时间看手机”的学生有
位，
由此可得补充完整的
列联表如下：
近视 | 不近视 | 合计 | ||
长时间看手机 | 65 | 10 | 75 | |
不长时间看手机 | 10 | 15 | 25 | |
合计 | 75 | 25 | 100 |
因此
的观测值
，
所以在犯错误的概率不超过
的前提下认为该校学生长时间看手机与近视有关．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】在一次抽样调查中测得样本的6组数据，得到一个变量
关于
的回归方程模型，其对应的数值如下表：
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数
加以说明与之间存在线性相关关系(当
时，说明与之间具有线性相关关系)；
(2)根据(1)的判断结果，建立关于的回归方程并预测当
时，对应的值为多少(
精确到
).
附参考公式：回归方程
中斜率和截距的最小二乘法估计公式分别为：
，
，相关系数公式为：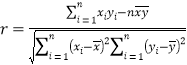
.
参考数据：
，
，
，
.
