ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Τσ“Β…ζ≤ζ“Μ÷÷≤ζΤΖΘ§ΗυΨίΨ≠―ιΘ§Τδ¥ΈΤΖ¬ ![]() ”κ»’≤ζΝΩ
”κ»’≤ζΝΩ![]() Θ®ΆρΦΰΘ©÷°Φδ¬ζΉψΙΊœΒ,
Θ®ΆρΦΰΘ©÷°Φδ¬ζΉψΙΊœΒ, Θ®Τδ÷–
Θ®Τδ÷–![]() ΈΣ≥Θ ΐΘ§«“
ΈΣ≥Θ ΐΘ§«“![]() Θ§“―÷ΣΟΩ…ζ≤ζ1ΆρΦΰΚœΗώΒΡ≤ζΤΖ“‘”·άϊ2Άρ‘ΣΘ§ΒΪΟΩ…ζ≤ζ1ΆρΦΰ¥ΈΤΖΫΪΩςΥπ1Άρ‘ΣΘ®ΉΔ:¥ΈΤΖ¬ =¥ΈΤΖ ΐ/…ζ≤ζΝΩΘ§ »γ
Θ§“―÷ΣΟΩ…ζ≤ζ1ΆρΦΰΚœΗώΒΡ≤ζΤΖ“‘”·άϊ2Άρ‘ΣΘ§ΒΪΟΩ…ζ≤ζ1ΆρΦΰ¥ΈΤΖΫΪΩςΥπ1Άρ‘ΣΘ®ΉΔ:¥ΈΤΖ¬ =¥ΈΤΖ ΐ/…ζ≤ζΝΩΘ§ »γ![]() ±μ ΨΟΩ…ζ≤ζ10Φΰ≤ζΤΖΘ§”–1Φΰ¥ΈΤΖΘ§Τδ”ύΈΣΚœΗώΤΖΘ©.
±μ ΨΟΩ…ζ≤ζ10Φΰ≤ζΤΖΘ§”–1Φΰ¥ΈΤΖΘ§Τδ”ύΈΣΚœΗώΤΖΘ©.
Θ®1Θ© ‘ΫΪ…ζ≤ζ’β÷÷≤ζΤΖΟΩΧλΒΡ”·άϊΕν![]() Θ®Άρ‘ΣΘ©±μ ΨΈΣ»’≤ζΝΩ
Θ®Άρ‘ΣΘ©±μ ΨΈΣ»’≤ζΝΩ![]() Θ®ΆρΦΰΘ©ΒΡΚ· ΐΘΜ
Θ®ΆρΦΰΘ©ΒΡΚ· ΐΘΜ
Θ®2Θ©Β±»’≤ζΝΩΈΣΕύ…Ό ±Θ§Ω…ΜώΒΟΉν¥σάϊ»σ?
ΓΨ¥πΑΗΓΩΘ®1Θ©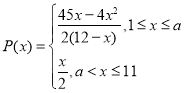 ΘΜΘ®2Θ©ΦϊΫβΈω.
ΘΜΘ®2Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©‘Υ”ΟΟΩΧλΒΡ”°άϊΈΣPΘ®xΘ©ΘΫ»’≤ζΝΩΘ®xΘ©ΓΝ’ΐΤΖ¬ Θ®1©¹QΘ©ΓΝ2©¹»’≤ζΝΩΘ®xΘ©ΓΝ¥ΈΤΖ¬ Θ®QΘ©ΓΝ1Θ§’ϊάμΦ¥Ω…ΒΟΒΫPΘ®xΘ©”κxΒΡΚ· ΐ ΫΘΜ
Θ®2Θ©Β±aΘΦxΓή11 ±Θ§«σΒΟPΘ®xΘ©ΒΡΉν¥σ÷ΒΘΜΒ±1ΓήxΓήa ±Θ§…η12©¹xΘΫtΘ§άϊ”ΟΜυ±Ψ≤ΜΒ» ΫΩ…ΒΟxΘΫ9 ±Θ§Β»Κ≈≥…ΝΔΘ§Ι Ω…Ζ÷άύΧ÷¬έΒΟΘΚΒ±1ΘΦaΘΦ3 ±Θ§Β±xΘΫ11 ±Θ§»ΓΒΟΉν¥σάϊ»σΘΜ 3ΓήaΘΦ9 ±Θ§‘Υ”ΟΗ¥ΚœΚ· ΐΒΡΒΞΒς–‘Ω…ΒΟΒ±xΘΫa ±»ΓΒΟΉν¥σάϊ»σΘΜΒ±9ΓήaΓή11 ±Θ§Β±»’≤ζΝΩΈΣ9ΆρΦΰ ±Θ§»ΓΒΟΉν¥σάϊ»σΘ°
Θ®1Θ©Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Γύ![]() .
.
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Γύ![]() .
.
Ήέ…œΘ§»’”·άϊΕν![]() Θ®Άρ‘ΣΘ©”κ»’≤ζΝΩxΘ®ΆρΦΰΘ©ΒΡΚ· ΐΙΊœΒ ΫΈΣ
Θ®Άρ‘ΣΘ©”κ»’≤ζΝΩxΘ®ΆρΦΰΘ©ΒΡΚ· ΐΙΊœΒ ΫΈΣ
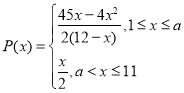 Θ§Θ®Τδ÷–aΈΣ≥Θ ΐΘ§«“
Θ§Θ®Τδ÷–aΈΣ≥Θ ΐΘ§«“![]() Θ©.
Θ©.
Θ®2Θ©Β±![]() ±Θ§
±Θ§![]() Θ§ΤδΉν¥σ÷ΒΈΣ55Άρ‘Σ.
Θ§ΤδΉν¥σ÷ΒΈΣ55Άρ‘Σ.
Β±![]() ±Θ§
±Θ§![]() Θ§…η
Θ§…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
¥Υ ±Θ§![]() Θ§
Θ§
œ‘»ΜΘ§Β±«“ΫωΒ±![]() Θ§Φ¥
Θ§Φ¥![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷ΒΘ§ΈΣ13.5Άρ‘Σ.
”–Ήν¥σ÷ΒΘ§ΈΣ13.5Άρ‘Σ.
Νν![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
ΫβΒΟ![]() Θ®…α»ΞΘ©Μρ
Θ®…α»ΞΘ©Μρ![]() Θ§
Θ§
‘ρΘ®iΘ©Β±![]() ±Θ§»’≤ζΝΩΈΣ11ΆρΦΰ ±Θ§Ω…ΜώΒΟΉν¥σάϊ»σ5.5Άρ‘Σ.
±Θ§»’≤ζΝΩΈΣ11ΆρΦΰ ±Θ§Ω…ΜώΒΟΉν¥σάϊ»σ5.5Άρ‘Σ.
Θ®iiΘ©Β±![]() ±Θ§
±Θ§![]() ±Θ§
±Θ§
Κ· ΐ![]() Ω…Ω¥≥… «”…Κ· ΐ
Ω…Ω¥≥… «”…Κ· ΐ![]() ”κ
”κ![]() Η¥ΚœΕχ≥…ΒΡ.
Η¥ΚœΕχ≥…ΒΡ.
“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Ι
Θ§Ι ![]() ‘Ύ
‘Ύ![]() …œΈΣΦθΚ· ΐ
…œΈΣΦθΚ· ΐ
”÷![]() ‘Ύ
‘Ύ![]() …œΈΣΦθΚ· ΐΘ§Υυ“‘
…œΈΣΦθΚ· ΐΘ§Υυ“‘![]() ‘Ύ
‘Ύ![]() …œΈΣ‘ωΚ· ΐ
…œΈΣ‘ωΚ· ΐ
Ι Β±»’≤ζΝΩΈΣaΆρΦΰ ±Θ§Ω…ΜώΒΟΉν¥σάϊ»σ![]() Άρ‘Σ.
Άρ‘Σ.
Θ®iiiΘ©Β±![]() ±Θ§»’≤ζΝΩΈΣ9ΆρΦΰ ±Θ§Ω…ΜώΒΟΉν¥σάϊ»σ13.5Άρ‘Σ.
±Θ§»’≤ζΝΩΈΣ9ΆρΦΰ ±Θ§Ω…ΜώΒΟΉν¥σάϊ»σ13.5Άρ‘Σ.

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ‘ΎΥΡάβΉΕ![]() ÷–Θ§
÷–Θ§![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§ΤΫΟφ
÷–ΒψΘ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°

Θ®1Θ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷ΒΘ°
ΒΡ”ύœ“÷ΒΘ°
ΓΨΧβΡΩΓΩΡ≥―ß–ΘΈΣΒς≤ιΗΟ–Θ―ß…ζΟΩ÷ή Ι”Ο ÷Μζ…œΆχΒΡ ±ΦδΘ§ΥφΜζ ’Φ·ΝΥ»τΗ…ΈΜ―ß…ζΟΩ÷ή Ι”Ο ÷Μζ…œΆχΒΡ ±ΦδΒΡ―υ±Ψ ΐΨίΘ®ΒΞΈΜΘΚ–Γ ±Θ©Θ§ΫΪ―υ±Ψ ΐΨίΖ÷ΉιΈΣ![]() Θ§Μφ÷ΤΝΥ»γœ¬ΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§“―÷Σ
Θ§Μφ÷ΤΝΥ»γœ¬ΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§“―÷Σ![]() ΡΎΒΡ―ß…ζ”–5»ΥΘ°
ΡΎΒΡ―ß…ζ”–5»ΥΘ°

Θ®1Θ©«σ―υ±Ψ»ίΝΩ![]() Θ§≤ΔΙάΦΤΗΟ–Θ―ß…ζΟΩ÷ήΤΫΨυ Ι”Ο ÷Μζ…œΆχΒΡ ±ΦδΘΜ
Θ§≤ΔΙάΦΤΗΟ–Θ―ß…ζΟΩ÷ήΤΫΨυ Ι”Ο ÷Μζ…œΆχΒΡ ±ΦδΘΜ
Θ®2Θ©ΫΪ Ι”Ο ÷Μζ…œΆχΒΡ ±Φδ‘Ύ![]() ΡΎΕ®“εΈΣΓΑ≥Λ ±ΦδΩ¥ ÷ΜζΓ±ΘΜ Ι”Ο ÷Μζ…œΆχΒΡ ±Φδ‘Ύ
ΡΎΕ®“εΈΣΓΑ≥Λ ±ΦδΩ¥ ÷ΜζΓ±ΘΜ Ι”Ο ÷Μζ…œΆχΒΡ ±Φδ‘Ύ![]() ΡΎΕ®“εΈΣΓΑ≤Μ≥Λ ±ΦδΩ¥ ÷ΜζΓ±Θ°“―÷Σ‘Ύ―υ±Ψ÷–”–
ΡΎΕ®“εΈΣΓΑ≤Μ≥Λ ±ΦδΩ¥ ÷ΜζΓ±Θ°“―÷Σ‘Ύ―υ±Ψ÷–”–![]() ΈΜ―ß…ζ≤ΜΫϋ ”Θ§Τδ÷–ΓΑ≤Μ≥Λ ±ΦδΩ¥ ÷ΜζΓ±ΒΡ”–
ΈΜ―ß…ζ≤ΜΫϋ ”Θ§Τδ÷–ΓΑ≤Μ≥Λ ±ΦδΩ¥ ÷ΜζΓ±ΒΡ”–![]() ΈΜ―ß…ζΘ°«κΫΪœ¬ΟφΒΡ
ΈΜ―ß…ζΘ°«κΫΪœ¬ΟφΒΡ![]() Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ
Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤Δ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ![]() ΒΡ«ΑΧαœ¬»œΈΣΗΟ–Θ―ß…ζ≥Λ ±ΦδΩ¥ ÷Μζ”κΫϋ ””–ΙΊΘ°
ΒΡ«ΑΧαœ¬»œΈΣΗΟ–Θ―ß…ζ≥Λ ±ΦδΩ¥ ÷Μζ”κΫϋ ””–ΙΊΘ°
Ϋϋ ” | ≤ΜΫϋ ” | ΚœΦΤ | |
≥Λ ±ΦδΩ¥ ÷Μζ | |||
≤Μ≥Λ ±ΦδΩ¥ ÷Μζ | 15 | ||
ΚœΦΤ | 25 |
≤ΈΩΦΙΪ ΫΚΆ ΐΨίΘΚ![]() Θ°
Θ°
|
|
|
|
|
|
|
|
|
|
|
|