Question

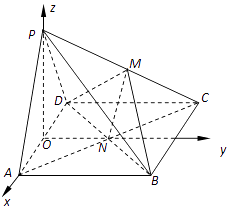
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，面PAD⊥底面ABCD，且△PAD是边长为2的等边三角形，PC= ，M在PC上，且PA∥面BDM．
（1）求直线PC与平面BDM所成角的正弦值；
（2）求平面BDM与平面PAD所成锐二面角的大小．

Answer 1

【答案】
（1）解：∵面PAD⊥面ABCD，△PAD为正三角形，作AD边上的高PO，

∵面PAD∩面ABCD=AD，由面面垂直的性质定理，得PO⊥面ABCD，

又ABCD是矩形，同理可得CD⊥面PAD，知CD⊥PD，

∵PC= ，PD=2，∴CD=3．

以AD中点O为坐标原点，OA所在直线为x轴，OP所在直线为z轴，AD的垂直平分线为y轴，建立如图所示的坐标系，

则P（0，0， ），A（1，0，0），B（1，3，0），C（﹣1，3，0），D（﹣1，0，0），

连结AC交BD于点N，由PA∥面MBD，面APC∩面MBD=MN，

∴MN∥PA，又N是AC的中点，

∴M是PC的中点，则M（ ， ， ），

设面BDM的法向量为 ，

， ，

则 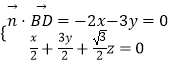，令x=1，解得y=﹣ ，z= ，得 ．

设PC与面BDM所成的角为θ，则 ，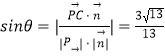

∴直线PC与平面BDM所成角的正弦值为 ．

（2）面PAD的法向量为向量 ，设面BDM与面PAD所成的锐二面角为φ，

则cosφ= ，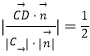

故平面BDM与平面PAD所成锐二面角的大小为 ．

【解析】作AD边上的高PO，由已知结合面面垂直的性质可得PO⊥面ABCD，再由ABCD是矩形，得到CD⊥PD，求解直角三角形可得CD．以AD中点O为坐标原点，OA所在直线为x轴，OP所在直线为z轴，AD的垂直平分线为y轴，建立空间直角坐标系，求出所用点的坐标，得到平面BDM的法向量 ．（1）设PC与面BDM所成的角为θ，由sinθ=| 求得直线PC与平面BDM所成角的正弦值．（2）求出平面PAD的法向量 ，由两平面法向量所成角的余弦值求得平面BDM与平面PAD所成锐二面角的大小．
【考点精析】关于本题考查的空间角的异面直线所成的角，需要了解已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则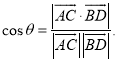才能得出正确答案．