Question

【题目】如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且 ，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG=2

（1）证明：AG∥平面BDE；
（2）求平面BDE和平面BAG所成锐二面角的余弦值．

Answer 1

【答案】
（1）证明：由平面ABCD⊥平面BCEG，平面ABCD∩平面BCEG=BC，CE⊥BC，

CE平面BCEG，

∴EC⊥平面ABCD．

根据题意建立如图所示的空间直角坐标系，

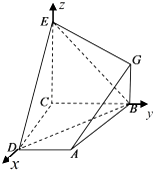
可得B（0，2，0），D（2，0，0），E（0，0，2），

A（2，1，0）G（0，2，1）…．（3分）

设平面BDE的法向量为 ，

∵ ，

∴ ，

即 ，

∴x=y=z，

∴平面BDE的一个法向量为

∵

∴ ，

∴ ，

∵AG平面BDE，∴AG∥平面BDE．

（2）解：设平面BAG的法向量为 ，平面BDE和平面BAG所成锐二面角为θ

因为 ， ，

由 得 ，

∴平面BAG的一个法向量为 ，

∴ ．

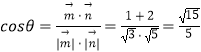故平面BDE和平面BAG所成锐二面角的余弦值为

【解析】（1）建立空间坐标系，求出平面的法向量，利用向量法即可证明AG∥平面BDE；（2）求出平面的法向量，利用向量法即可求平面BDE和平面BAG所成锐二面角的余弦值．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．