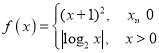题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,设M,N是椭圆C上位于x轴上方的两动点,且直线
,设M,N是椭圆C上位于x轴上方的两动点,且直线![]() 与直线
与直线![]() 平行,
平行,![]() 与
与![]() 交于点D.
交于点D.
(Ⅰ)求![]() 和
和![]() 的坐标;
的坐标;
(Ⅱ)求![]() 的最小值;
的最小值;
(Ⅲ)求证:![]() 是定值.
是定值.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】
(Ⅰ)由椭圆方程得![]() 后可得
后可得![]() ,即得焦点坐标;
,即得焦点坐标;
(Ⅱ)设直线![]() 与椭圆的另一焦点是
与椭圆的另一焦点是![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,设
,设![]() ,设直线
,设直线![]() 方程是
方程是![]() ,与椭圆方程联立消元后应用韦达定理可得
,与椭圆方程联立消元后应用韦达定理可得![]() ,用弦长公式求得
,用弦长公式求得![]() ,计算
,计算![]() 并代入
并代入![]() 得关于
得关于![]() 的函数,可得最小值.
的函数,可得最小值.
(Ⅲ)由(Ⅱ)得![]() ,再由
,再由![]() ,由平行线性质求得
,由平行线性质求得![]() 和
和![]() ,相加即证.
,相加即证.
(Ⅰ)由题意![]() ,
,![]() ,所以
,所以![]() ,焦点为
,焦点为![]() ,
,![]() ;
;
(Ⅱ)设直线![]() 与椭圆的另一焦点是
与椭圆的另一焦点是![]() ,因为
,因为![]() ,所以由椭圆的对称性得
,所以由椭圆的对称性得![]() ,
,
设![]() ,设直线
,设直线![]() 方程是
方程是![]() ,
,
由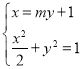 得
得![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
所以当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.
(Ⅲ)因为![]() ,且
,且![]() 在椭圆上,
在椭圆上,
所以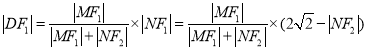
同理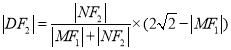 ,
,
所以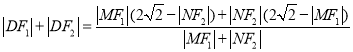
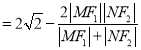 ,
,
由(Ⅱ)![]() ,
,
![]()
![]()
![]() ,
,
所以![]()
![]() 为定值.
为定值.

【题目】随着节能减排意识深入人心以及共享单车在饶城的大范围推广,越来越多的市民在出行时喜欢选择骑行共享单车。为了研究广大市民在共享单车上的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果认为每周使用超过3次的用户为“喜欢骑行共享单车”,请完成![]() 列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,视频率为概率,在我市所有“骑行达人”中,随机抽取4名用户.
① 求抽取的4名用户中,既有男生“骑行达人”又有女“骑行达人”的概率;
②为了鼓励女性用户使用共享单车,对抽出的女“骑行达人”每人奖励500元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式: 
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记![]() 表示1台机器在三年使用期内的保养次数.
表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“![]() 不超过2”的概率;
不超过2”的概率;
(2)若![]() 表示1台机器的售价和三年使用期内花费的费用总和(单位:元),求选用方案一时
表示1台机器的售价和三年使用期内花费的费用总和(单位:元),求选用方案一时![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?