题目内容
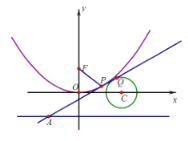
【题目】在棱长为1的正方体
中，E，F分别为线段CD和
上的动点，且满足
，则四边形
所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（ ）
A. 有最小值
B. 有最大值
C. 为定值3D. 为定值2
【答案】D
【解析】
分别在后，上，左三个平面得到该四边形的投影，求其面积和即可．
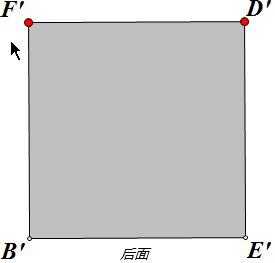
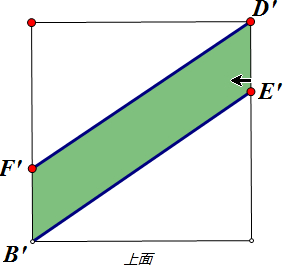
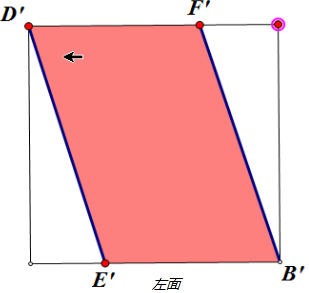
依题意，设四边形D1FBE的四个顶点在后面，上面，左面的投影点分别为D'，F'，B'，E'，则四边形D1FBE在上面，后面，左面的投影分别如上图．
所以在后面的投影的面积为S后=1×1=1，
在上面的投影面积S上=D'E'×1=DE×1=DE，
在左面的投影面积S左=B'E'×1=CE×1=CE，
所以四边形D1FBE所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和
S=S后+S上+S左=1+DE+CE=1+CD=2．
故选：D．
练习册系列答案
相关题目
