题目内容
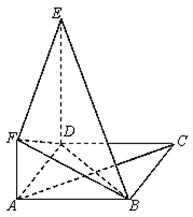
如图所示,正方形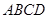 与直角梯形
与直角梯形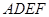 所在平面互相垂直,
所在平面互相垂直,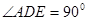 ,
, ,
,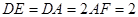 .
.
(1)求证: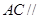 平面
平面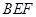 ;
;
(2)求四面体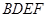 的体积.
的体积.
(1)证明:见解析;(2)四面体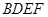 的体积
的体积
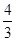 .
.
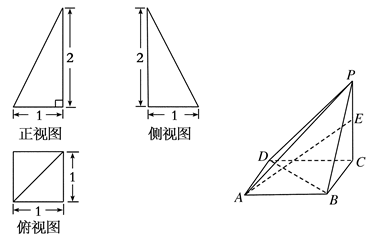
解析试题分析:(1)设正方形ABCD的中心为O,取BE中点G,连接FG,OG,由中位线定理,我们易得四边形AFGO是平行四边形,即FG∥OA,由直线与平面平行的判定定理即可得到AC∥平面BEF;
(2)由已知中正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,我们可以得到AB⊥平面ADEF,结合DE=DA=2AF=2.分别计算棱锥的底面面积和高,代入棱锥体积公式即可求出四面体BDEF的体积.(1)的关键是证明出FG∥OA,(2)的关键是得到AB⊥平面ADEF,即四面体BDEF的高为AB.
试题解析:(1)证明:设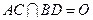 ,取
,取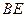 中点
中点 ,
,
连结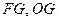 ,所以,
,所以,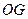

因为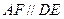 ,
,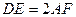 ,所以
,所以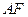
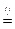
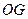 ,
,
从而四边形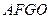 是平行四边形,
是平行四边形, . 2分
. 2分
因为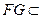 平面
平面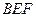 ,
,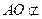 平面
平面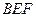 , 4分
, 4分
所以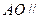 平面
平面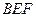 ,即
,即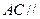 平面
平面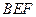 . 6分
. 6分
(2)解:因为平面
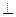 平面
平面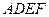 ,
,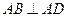 ,
,
所以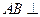 平面
平面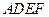 . 8分
. 8分
因为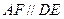 ,
,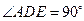 ,
,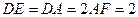 ,
,
所以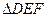 的面积为
的面积为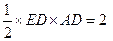 , 10分
, 10分
所以四面体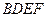 的体积
的体积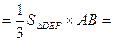
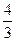 . 12分
. 12分
考点:1.直线与平面平行的判定;2.棱锥的体积

练习册系列答案
相关题目
 中,
中,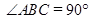 ,
,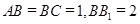 ,求:
,求: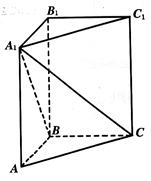
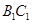 与
与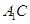 所成角的大小;
所成角的大小; 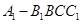 的体积.
的体积.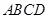 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面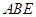 ,
, ,
, ,
,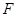 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE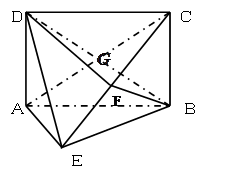
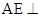 平面
平面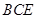 ;
;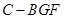 的体积.
的体积.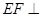 平面
平面 ,
, ,
,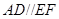 ,
,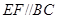 ,
,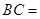
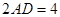 ,
,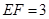 ,
,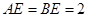 ,
,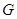 是
是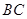 的中点.
的中点.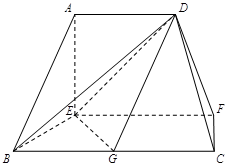
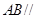 平面
平面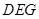 ;
;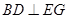 ;
;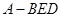 的体积.
的体积.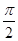 .
.
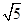 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积. 中,
中,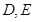 分别是
分别是 的中点,
的中点,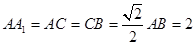 .
.
 ;
;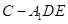 的体积.
的体积.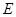 是矩形
是矩形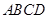 中
中 边上的点,
边上的点,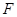 为
为 边的中点,
边的中点,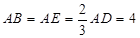 ,现将
,现将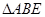 沿
沿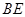 边折至
边折至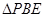 位置,且平面
位置,且平面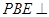 平面
平面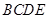 .
.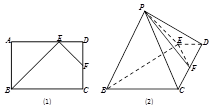
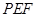 ;
;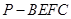 的体积.
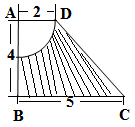
的体积. 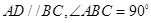 ,求图中阴影部分绕A
,求图中阴影部分绕A B旋转一周形成的几何体的表面积和体积.
B旋转一周形成的几何体的表面积和体积.