题目内容
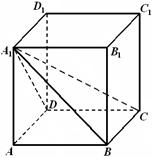
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=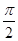 .
.
(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=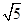 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
(1)证明详见解析;(2)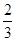
解析试题分析:(1)连结AB1,则AC⊥BA1.,又∵AB=AA1,∴四边形ABB1A1是正方形,∴BA1⊥AB1,由直线与平面垂直的判定定理可的BA1⊥平面CAB1,故CB1⊥BA1.(2)首先求出A1C1的值,由(1)知,A1C1⊥平面ABA1,即A1C1是三棱锥C1-ABA1的高,然后在求出△ABA1的面积,最后根据棱锥的体积公式求解即可.
试题解析:解:(1)证明:如图,连结AB1,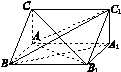
∵ABC-A1B1C1是直三棱柱,∠CAB=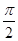 ,
,
∴AC⊥平面ABB1A1,故AC⊥BA1. 3分
又∵AB=AA1,∴四边形ABB1A1是正方形,
∴BA1⊥AB1,又CA∩AB1=A.
∴BA1⊥平面CAB1,故CB1⊥BA1. 6分
(2)∵AB=AA1=2,BC=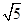 ,∴AC=A1C1=1, 8分
,∴AC=A1C1=1, 8分
由(1)知,A1C1⊥平面ABA1, 10分
∴VC1-ABA1=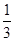 S△ABA1·A1C1=
S△ABA1·A1C1=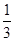 ×2×1=
×2×1=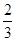 . 12分
. 12分
考点:1.直棱柱的性质和直线与平面垂直的判定;2.棱锥的体积.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 的棱长为
的棱长为 .
.
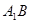 与
与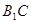 所成角的大小;
所成角的大小;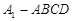 的体积.
的体积.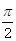 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .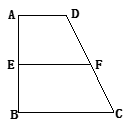
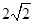 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.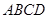 与直角梯形
与直角梯形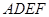 所在平面互相垂直,
所在平面互相垂直,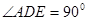 ,
, ,
,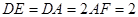 .
.
 平面
平面 ;
; 的体积.
的体积.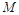 是
是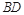 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.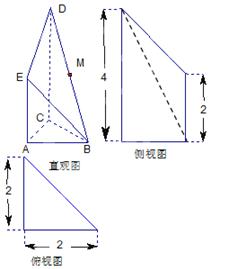
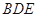 ? 若存在,确定
? 若存在,确定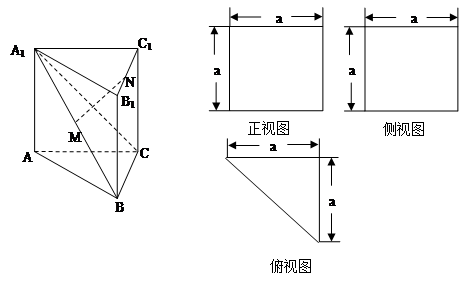
 是棱长为
是棱长为 的正方体,
的正方体, 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且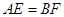 .
.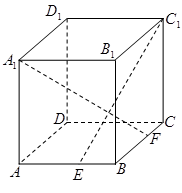
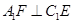 ;
;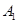 、
、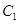 共面时,求:面
共面时,求:面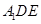 与面
与面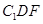 所成二面角的余弦值.
所成二面角的余弦值.