题目内容
在直三棱柱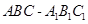 中,
中,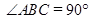 ,
,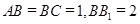 ,求:
,求: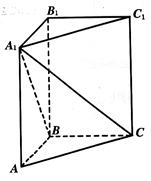
(1)异面直线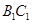 与
与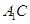 所成角的大小;
所成角的大小;
(2)四棱锥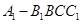 的体积.
的体积.
(1)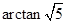 ;(2)
;(2)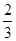 .
.
解析试题分析:(1)求异面直线所成的角,就是根据定义作出这个角,当然异面直线的平移,一般是过其中一条上的一点作另一条的平行线,特别是在基本几何体中,要充分利用几何体中的平行关系寻找平行线,然后在三角形中求解,本题中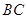 ∥
∥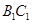 ,
,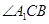 就是我们要求的角(或其补角);(2)一种方法就是直接利用体积公式,四棱锥
就是我们要求的角(或其补角);(2)一种方法就是直接利用体积公式,四棱锥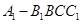 的底面是矩形
的底面是矩形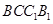 ,下面要确定高,即找到底面
,下面要确定高,即找到底面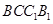 的垂线,由于是直棱柱,因此侧棱
的垂线,由于是直棱柱,因此侧棱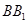 与底面垂直,从而
与底面垂直,从而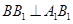 ,题中又有
,题中又有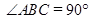 ,即
,即 ,从而
,从而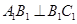 ,故
,故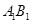 就是底面的垂线,也即高.
就是底面的垂线,也即高.
试题解析:(1)因为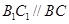 ,所以
,所以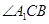 (或其补角)是异面直线
(或其补角)是异面直线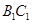 与
与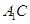 所成角. 1分
所成角. 1分
因为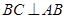 ,
,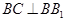 ,所以
,所以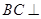 平面
平面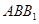 ,所以
,所以 . 3分
. 3分
在 中,
中,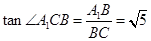 ,所以
,所以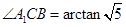 5分
5分
所以异面直线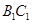 与
与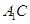 所成角的大小为
所成角的大小为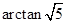 . 6分
. 6分
(2)因为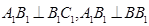
所以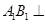 平面
平面 9分
9分
则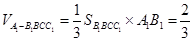 12分
12分
考点:(1)异面直线所成的角;(2)求体积.

练习册系列答案
相关题目
 所在的平面和平面
所在的平面和平面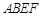 互相垂直,等腰梯形
互相垂直,等腰梯形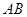 ∥
∥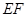 ,
,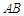 =2,
=2,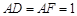 ,
,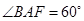 ,
,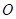 ,
, 分别为
分别为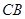 的中点,
的中点,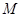 为底面
为底面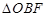 的重心.
的重心.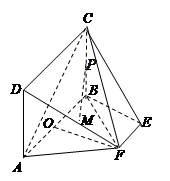
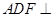 平面
平面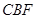 ;
;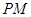 ∥平面
∥平面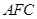 ;
; 的体积
的体积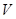 .
. 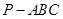 中,
中,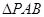 和
和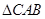 都是以
都是以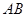 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,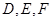 分别是
分别是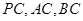 的中点.
的中点.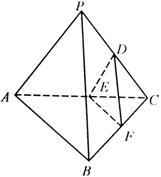
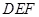 //平面
//平面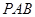 ;
;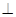
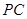 ;
;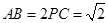 ,求三棱锥
,求三棱锥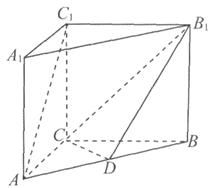

 中,底面
中,底面 是菱形,
是菱形,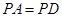 ,
,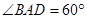 ,
,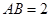 ,
,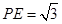 ,
,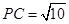 ,
,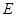 是
是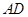 的中点,
的中点,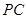 上的点
上的点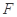 满足
满足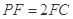 .
.
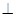 平面
平面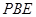 ;
;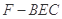 的体积.
的体积.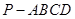 中,底面
中,底面 是菱形,
是菱形,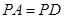 ,
,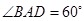 ,
,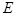 是
是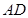 的中点,点
的中点,点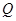 在侧棱
在侧棱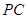 上.
上.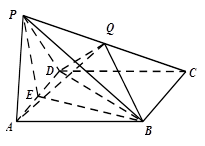
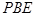 ;
; //平面
//平面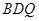 ;
;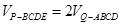 ,试求
,试求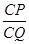 的值.
的值.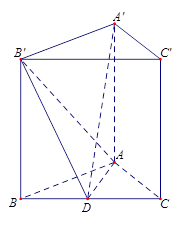
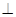 B'D;
B'D;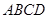 与直角梯形
与直角梯形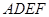 所在平面互相垂直,
所在平面互相垂直,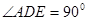 ,
, ,
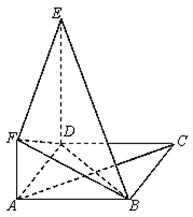
,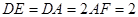 .
.
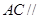 平面
平面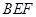 ;
;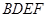 的体积.
的体积.