题目内容
【题目】某学校为调查高三年级学生的身高情况，按随机抽样的方法抽取100名学生，得到男生身高情况的频率分布直方图（图（1））和女生身高情况的频率分布直方图（图（2））.已知图（1）中身高在
的男生人数有16人.
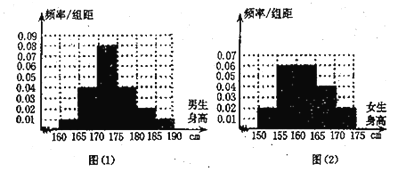
（1）试问在抽取的学生中，男，女生各有多少人？
（2）根据频率分布直方图，完成下列的
列联表，并判断能有多大（百分之几）的把握认为“身高与性别有关”？
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
（3）在上述100名学生中，从身高在
之间的男生和身高在之间的女生中间按男、女性别分层抽样的方法，抽出6人，从这6人中选派2人当旗手，求2人中恰好有一名女生的概率.
参考公式：
参考数据：
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
【答案】（1）40,60；（2）列联表见解析，有
的把握认为身高与性别有关；（3）
.
【解析】
（1）根据直方图求出男生的人数为40，再求女生的人数；（2）完成列联表，再利用独立性检验求出有的把握认为身高与性别有关；（3）利用古典概型的概率公式求出2人中恰好有一名女生的概率.
（1）直方图中，因为身高在
的男生的频率为0.4，
设男生数为
，则
，得
.
由男生的人数为40，得女生的人数为
.
（2）男生身高
的人数
，
女生身高的人数
，
所以可得到下列列联表：
|
| 总计 | ||
男生身高 | 30 | 10 | 40 | |
女生身高 | 6 | 54 | 60 | |
总计 | 36 | 64 | 100 |
，
所以能有的把握认为身高与性别有关；
（3）在
之间的男生有12人，在之间的女生人数有6人.
按分层抽样的方法抽出6人，则男生占4人，女生占2人.
设男生为
，
，
，
，女生为
，
.
从6人任选2名有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共15种可能，
2人中恰好有一名女生：，，，，，，，共8种可能，
故所求概率为
.
练习册系列答案
相关题目
