题目内容
【题目】某学校在学校内招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者.将这
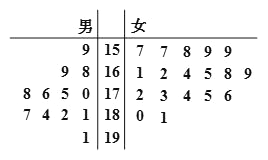
名女志愿者.将这![]() 名志愿者的身高编成如右茎叶图(单位:
名志愿者的身高编成如右茎叶图(单位: ![]() ),若身高在
),若身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(Ⅰ)如果用分层抽样的方法从“高个子”和“非高个子”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,那么至少有一人是“高个子”的概率是多少?
人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中选![]() 名志愿者,用
名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:(Ⅰ)根据茎叶图,有“高个子”12人,“非高个子”18人,利用分层抽样的方法所抽取的“高个子”的人数为![]() 人,进而可求得“至少有一人是“高个子”的概率;
人,进而可求得“至少有一人是“高个子”的概率;
(Ⅱ)依题意知,“女高个子”的人数为![]() 人,随机变量
人,随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,计算取每个值的概率,得出分布列,利用公式即可求解数学期望.
,计算取每个值的概率,得出分布列,利用公式即可求解数学期望.
试题解析:
(Ⅰ)根据茎叶图,有“高个子”12人,“非高个子”18人,
所以利用分层抽样的方法所抽取的“高个子”的人数为![]() 人,
人,
抽取的“非高个子”的人数为![]() 人,
人,
设“至少有一人是“高个子””为事件![]() ,
,
则![]() ,
,
即至少有一人是“高个子”的概率为![]() .
.
(Ⅱ)依题意知,“女高个子”的人数为![]() 人,随机变量
人,随机变量![]() 的所有可能取值为
的所有可能取值为![]() .
.
![]()
![]() ,
,
![]() ,
,
![]() .
.
随机变量![]() 的分布列是:
的分布列是:
|
|
|
|
|
|
|
|
|
|
数学期望![]() .
.

【题目】某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| a |
|
第3组 |
| 30 | b |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
| |
![]() Ⅰ
Ⅰ![]() 求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
求出频率分布表中a,b的值,再在答题纸上完成频率分布直方图;
![]() Ⅱ
Ⅱ![]() 根据样本频率分布直方图估计样本成绩的中位数;
根据样本频率分布直方图估计样本成绩的中位数;
![]() Ⅲ
Ⅲ![]() 高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.
高校决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,再从6名学生中随机抽取2名学生由A考官进行面试,求第4组至少有一名学生被考官A面试的概率.