题目内容
【题目】如图,三棱柱![]() 中,侧棱垂直底面,
中,侧棱垂直底面,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
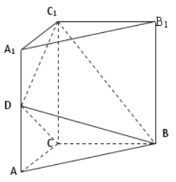
(Ⅰ)证明:平面![]() 平面
平面![]() .
.
(Ⅱ)平面![]() 分此棱柱为两部分,求这两部分体积比.
分此棱柱为两部分,求这两部分体积比.
【答案】(I)证明见解析;(II)![]() .
.
【解析】
试题分析:(I)易证得![]() 平面
平面![]() ,再由面面垂直的判定定理即可证得平面
,再由面面垂直的判定定理即可证得平面![]() 平面
平面![]() ;(II)设棱锥
;(II)设棱锥![]() 的体积为
的体积为![]() ,易求得
,易求得![]() ,三棱术
,三棱术![]() 的体积为
的体积为![]() ,于是得
,于是得![]() ,从而可得答案.
,从而可得答案.
试题解析: (I)由题意知BC⊥CC1,BC⊥AC,CC1∩AC=C,
∴BC⊥平面ACC1A1,又DC1![]() 平面ACC1A1,
平面ACC1A1,
∴DC1⊥BC.
由题设知∠A1DC1=∠ADC=45°,
∴∠CDC1=90°,即DC1⊥DC,又DC∩BC=C,
∴DC1⊥平面BDC,又DC1平面BDC1,
∴平面BDC1⊥平面BDC;
(II)设棱锥B﹣DACC1的体积为V1,AC=1,由题意得V1=![]() ×
×![]() ×1×1=
×1×1=![]() ,
,
又三棱柱ABC﹣A1B1C1的体积V=1,
∴(V﹣V1):V1=1:1,
∴平面BDC1分此棱柱两部分体积的比为1:1.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目