题目内容
【题目】正整数![]() ,
, ![]() ,
, ![]() 是等腰三角形的三边长,并且
是等腰三角形的三边长,并且![]() ,这样的三角形有( )个.
,这样的三角形有( )个.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】![]() 可以化为(a+b)(c+1)=24,其中a,b,c都是正整数,并且其中两个数相等,
可以化为(a+b)(c+1)=24,其中a,b,c都是正整数,并且其中两个数相等,
令a+b=A,c+1=C则A,C为大于2的正整数,
那么24分解为大于等于2的两个正整数的乘积有几种组合2×12,3×8,4×6,6×4,3×8,2×12,
①、A=2,C=12时,c=11,a+b=2,无法得到满足等腰三角形的整数解;
②、A=3,C=8时,c=7,a+b=3,无法得到满足等腰三角形的整数解;
③、A=4,C=6时,c=5,a+b=4,无法得到满足等腰三角形的整数解;
④、A=6,C=4时,c=3,a+b=6,可以得到a=b=c=3,可以组成等腰三角形;
⑤、A=8,C=3时,c=2,a+b=8,可得a=b=4,c=2,可以组成等腰三角形,a=b=4是两个腰;
⑥、A=12,C=2时,可得a=b=6,c=1,可以组成等腰三角形,a=b=6是两个腰。
∴一共有3个这样的三角形。
故选C.

【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
求数学成绩![]() 关于物理成绩
关于物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]()
若某位学生的物理成绩为80分,预测他的数学成绩;
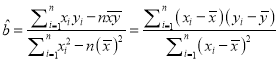
【题目】某中学为了解2017届高三学生的性别和喜爱游泳是否有关,对100名高三学生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.9%的把握认为喜欢游泳与性别有关?
附: 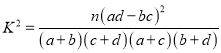
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |