[题目]已知二次函数的图像经过坐标原点.其到函数为.数列的前项和为.点均在函数的图像上． (I)求数列的通项公式,(Ⅱ)设.是数列的前n项和.求使得＜对所有都成立的最小正整数m. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知二次函数的图像经过坐标原点，其到函数为，数列的前项和为，点均在函数的图像上．

（I）求数列的通项公式；

（Ⅱ）设，是数列的前n项和，求使得＜对所有都成立的最小正整数m.

【答案】(I)；(II).

【解析】

试题分析：(I)设二次函数,根据导函数的表达式,再根据点均在函数的图象上,求出的递推公式；(II)把(I)中的递推关系式代入,根据裂项相消求得,最后解得使＜对所有都成立的最小正整数.

试题解析：（Ⅰ）设这二次函数，则，

由于，所以，所以，

又因为点均在函数的图像上，所以，

当时，，

当时，，也适合.

所以，.

（Ⅱ）由（Ⅰ）得

故

随着的增大，逐渐增大直至趋近，故﹤对所有都成立，只要即可，即只要.

故使得﹤对所有都成立的最小正整数.

练习册系列答案

(1)若A∩B的子集个数为4，求a的范围；

(2)若a∈Z，当A∩B≠时，求a的最小值，并求当a取最小值时A∪B.

【题目】某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：

年份	2011	2012	2013	2014	2015
储蓄存款（千亿元）	5	6	7	8	10

为了研究计算的方便，工作人员将上表的数据进行了处理，，得到下表2：

时间代号	1	2	3	4	5
	0	1	2	3	5

（Ⅰ）求关于的线性回归方程；

（Ⅱ）通过（Ⅰ）中的方程，求出关于的回归方程；

（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？

（附：对于线性回归方程）

【题目】设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若(A)∩B=,求m的值.

【题目】定义在上的函数满足：对任意、恒成立，当时，.

（1）求证在上是单调递增函数；

（2）已知，解关于的不等式；

（3）若，且不等式对任意恒成立.求实数的取值范围.

【题目】如图，三棱柱中，侧棱垂直底面，，，是棱的中点．

（Ⅰ）证明：平面平面．

（Ⅱ）平面分此棱柱为两部分，求这两部分体积比．

【题目】已知函数.

（1）若曲线在和处的切线互相平行，求的值；

（2）求的单调区间；

（3）设，若对任意，均存在，使得，求的取值范围.

【题目】已知全集

（1）若，求实数q的取值范围；

（2）若中有四个元素，求和q的值.

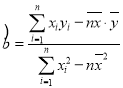
【题目】化为推出一款6寸大屏手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：

女性用户：

分值区间
频数	20	40	80	50	10

男性用户：

分值区间
频数	45	75	90	60	30

（1）如果评分不低于70分，就表示该用户对手机“认可”，否则就表示“不认可”，完成下列列联表，并回答是否有的把握认为性别对手机的“认可”有关：

	女性用户	男性用户	合计
“认可”手机
“不认可”手机
合计

附：

	0.05	0.01
	3.841	6.635

（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取2名用户，求2名用户中评分小于90分的概率．

试题分类