题目内容
3.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )
| A. | {x|-1<x≤0} | B. | {x|-1≤x≤1} | C. | {x|-1<x≤1} | D. | {x|-1<x≤2} |
分析 在已知坐标系内作出y=log2(x+1)的图象,利用数形结合得到不等式的解集.
解答 解:由已知f(x)的图象,在此坐标系内作出y=log2(x+1)的图象,如图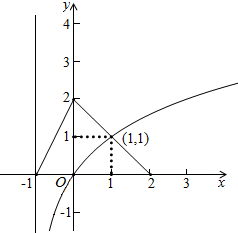
满足不等式f(x)≥log2(x+1)的x范围是-1<x≤1;所以不等式f(x)≥log2(x+1)的解集是{x|-1<x≤1};
故选C.
点评 本题考查了数形结合求不等式的解集;用到了图象的平移.

练习册系列答案
相关题目
13.函数f(x)的定义域为D,对给定的正数k,若存在闭区间[a,b]⊆D,使得函数f(x)满足:①f(x)在[a,b]内是单调函数;②f(x)在[a,b]上的值域为[ka,kb],则称区间[a,b]为y=f(x)的k级“理想区间”.下列结论错误的是( )
| A. | 函数f(x)=-x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=loga(ax-$\frac{1}{4}$)(a>0,a≠1)不存在4级“理想区间” |
14.现有10张奖券,其中8张2元,2张5元,今某人随机无放回的抽取三张,则此人得奖金金额的数学期望为( )
| A. | 6元 | B. | 12元 | C. | 7.8元 | D. | 9元 |