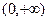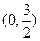题目内容
如果函数y=f(x)=2x3-3x2+a的极大值为6,那么a等于
| A.6 | B.0 |
| C.5 | D.1 |
A
本题主要考查应用导数解决有关极值与参数问题.
y′=f′(x)=6x2-6x,由于求极值,所以y′=0,即x2-x=0,解得x=0或1,列表如下:
所以y极大=f(0)=a=6,故选A.
y′=f′(x)=6x2-6x,由于求极值,所以y′=0,即x2-x=0,解得x=0或1,列表如下:
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| y′ | + | 0 | - | 0 | + |
| y | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |

练习册系列答案
相关题目
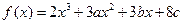 在
在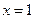 及
及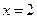 时取得极值.
时取得极值.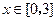 ,都有
,都有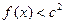 成立,求c的取值范围.
成立,求c的取值范围.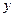 =
= 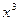 -12
-12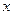 +16在 [-3,3]上的最大值、最小值分别是( )
+16在 [-3,3]上的最大值、最小值分别是( )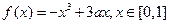 的最大值。
的最大值。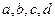 为何值时,函数
为何值时,函数 在
在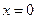 处有极大值
处有极大值 ,在
,在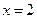 处有极小值
处有极小值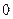 ?
?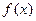 的定义域为开区间
的定义域为开区间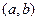 ,导函数
,导函数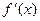 在
在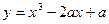 在
在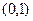 内有极小值,则实数
内有极小值,则实数 的取值范围为( )
的取值范围为( )