题目内容
9.从集合{1,2,3}中随机取一个元素,记为a,从集合{2,3,4}中随机取一个元素,记为b,则a≤b的概率为$\frac{8}{9}$.分析 先确定的所有的基本事件,共有9种,再求出a>b的概率,根据互斥事件的概率公式计算即可.
解答 解:从集合{1,2,3}中随机取一个元素,记为a,从集合{2,3,4}中随机取一个元素,共有3×3=9种,
因为a>b的取法只有一种:a=3,b=2,
所以a>b的概率是$\frac{1}{9}$,
所以a≤b的概率是1-$\frac{1}{9}$=$\frac{8}{9}$.
故答案为:$\frac{8}{9}$.
点评 本题考查了古典概型的概率和互斥事件的概率问题,属于基础题.

练习册系列答案
相关题目
4.已知|${\overrightarrow{OA}}$|=2,|${\overrightarrow{OB}}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,点C在AB上,∠AOC=30°.则向量$\overrightarrow{OC}$等于( )
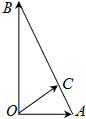

| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
18.能够把椭圆$\frac{{x}^{2}}{4}$+y2=1的周长和面积同时分为相等的两部分的函数称为椭圆的“可分函数”,下列函数不是椭圆的“可分函数”为( )
| A. | f(x)=4x3+x | B. | f(x)=ln$\frac{5-x}{5+x}$ | C. | f(x)=sin$\frac{x}{2}$ | D. | f(x)=ex+e-x |
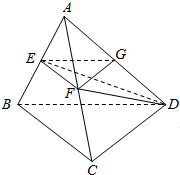 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证: