题目内容
5.已知等差数列{an}满足a1+a2=10,a4-a3=2(1)求{an}的通项公式;
(2)设等比数列{bn}满足b2=a3,b3=a7,问:b6与数列{an}的第几项相等?
分析 (I)由a4-a3=2,可求公差d,然后由a1+a2=10,可求a1,结合等差数列的通项公式可求
(II)由b2=a3=8,b3=a7=16,可求等比数列的首项及公比,代入等比数列的通项公式可求b6,结合(I)可求
解答 解:(I)设等差数列{an}的公差为d.
∵a4-a3=2,所以d=2
∵a1+a2=10,所以2a1+d=10
∴a1=4,
∴an=4+2(n-1)=2n+2(n=1,2,…)
(II)设等比数列{bn}的公比为q,
∵b2=a3=8,b3=a7=16,
∴$\left\{\begin{array}{l}{{b}_{1}q=8}\\{{b}_{1}{q}^{2}=16}\end{array}\right.$
∴q=2,b1=4
∴${b}_{6}=4×{2}^{6-1}$=128,而128=2n+2
∴n=63
∴b6与数列{an}中的第63项相等
点评 本题主要考查了等差数列与等比数列通项公式的简单应用,属于对基本公式应用的考查,试题比较容易.

练习册系列答案
相关题目
13.若集合E={(p,q,r,s)|0≤p<s≤4,0≤q<s≤4,0≤r<s≤4且p,q,r,s∈N},F={(t,u,v,w)|0≤t<u≤4,0≤v<w≤4且t,u,v,w∈N},用card(X)表示集合X中的元素个数,则 card(E)+card(F)=( )
| A. | 200 | B. | 150 | C. | 100 | D. | 50 |
20.某校老年、中年和青年教师的人数见如表,采用分层插样的方法调查教师的身体状况,在抽取的样本中,青年教师有320人,则该样本的老年教师人数为( )
| 类别 | 人数 |
| 老年教师 | 900 |
| 中年教师 | 1800 |
| 青年教师 | 1600 |
| 合计 | 4300 |
| A. | 90 | B. | 100 | C. | 180 | D. | 300 |
10.某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )


| A. | $\frac{8}{9π}$ | B. | $\frac{8}{27π}$ | C. | $\frac{24(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{8(\sqrt{2}-1)^{3}}{π}$ |
17.已知等比数列{an}满足a1=3,a1+a3+a5=21,则a3+a5+a7=( )
| A. | 21 | B. | 42 | C. | 63 | D. | 84 |
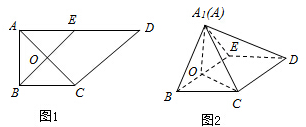 如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.