题目内容
10.某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )
| A. | $\frac{8}{9π}$ | B. | $\frac{8}{27π}$ | C. | $\frac{24(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{8(\sqrt{2}-1)^{3}}{π}$ |
分析 由题意,原材料对应的几何体是圆锥,其内接正方体是加工的新工件,求出它们的体积,正方体的体积与圆锥的体积比为所求.
解答 解:由题意,由工件的三视图得到原材料是圆锥,底面是直径为2的圆,母线长为3,所以圆锥的高为2$\sqrt{2}$,圆锥是体积为$\frac{1}{3}π×2\sqrt{2}=\frac{2\sqrt{2}π}{3}$;
其内接正方体的棱长为x,则$\frac{\sqrt{2}x}{2}=\frac{2\sqrt{2}-x}{2\sqrt{2}}$,解得x=$\frac{2\sqrt{2}}{3}$,所以正方体的体积为$(\frac{2\sqrt{2}}{3})^{3}=\frac{16\sqrt{2}}{27}$,
所以原工件材料的利用率为:$\frac{新工件的体积}{原工件的体积}$=$\frac{8}{9π}$;
故选:A.
点评 本题考查了由几何体的三视图得到几何体的体积以及几何体的内接正方体棱长的求法;正确还原几何体以及计算内接正方体的体积是关键,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
2.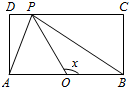 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 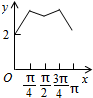 | B. | 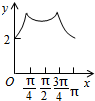 | C. | 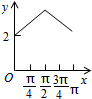 | D. | 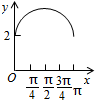 |
20.已知M(x0,y0)是双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点,F1,F2是C的左、右两个焦点,若$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$<0,则y0的取值范围是( )
| A. | $(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$ | B. | $(-\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{6})$ | C. | $(-\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3})$ | D. | $(-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3})$ |
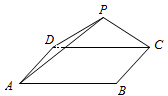 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3. 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,