题目内容
5.若函数f(x)=|1nx|-mx恰有3个零点,则m的取值范围为(0,$\frac{1}{e}$).分析 由题意可得函数y=|1nx|的图象和直线y=mx有3个交点.求出过原点和曲线y=lnx相切的切线的斜率的值,可得m的范围.
解答  解:由题意函数f(x)=|1nx|-mx恰有3个零点,
解:由题意函数f(x)=|1nx|-mx恰有3个零点,
可得函数y=|1nx|的图象和直线y=mx有3个交点.
设过原点和曲线y=lnx相切的切线的切点为
(a,lna),
则由切线斜率的几何意义可得切线的斜率
为y′|x=a=$\frac{1}{a}$=$\frac{lna-0}{a-0}$,求得a=e,
即此切线的斜率为$\frac{1}{e}$,∴0<m<$\frac{1}{e}$,
故答案为:$({0,\frac{1}{e}})$.
点评 本题主要考查方程根的存在性以及个数判断,切线斜率的几何意义,体现了数形结合、转化的数学思想,属于中档题.

练习册系列答案
相关题目
10. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
17.已知函数f(x)=sinπx和函数g(x)=cosπx在区间[0,2]上的图象交于A,B两点,则△OAB面积是( )
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
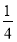 圆弧)( )
圆弧)( )
 B.
B.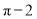
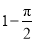 D.
D.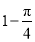

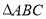 中,角
中,角 所对的边分别为
所对的边分别为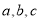 ,且
,且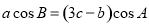 .
. ,求
,求 ;
; ,且
,且 的面积为
的面积为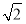 ,求
,求 的周长.
的周长.