题目内容
已知 ,
, 为其反函数.
为其反函数.
(Ⅰ)说明函数 与
与 图象的关系(只写出结论即可);
图象的关系(只写出结论即可);
(Ⅱ)证明 的图象恒在
的图象恒在 的图象的上方;
的图象的上方;
(Ⅲ)设直线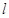 与
与 、
、 均相切,切点分别为(
均相切,切点分别为( )、(
)、( ),且
),且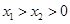 ,求证:
,求证: .
.
 ,
, 为其反函数.
为其反函数.(Ⅰ)说明函数
 与
与 图象的关系(只写出结论即可);
图象的关系(只写出结论即可);(Ⅱ)证明
 的图象恒在
的图象恒在 的图象的上方;
的图象的上方;(Ⅲ)设直线
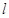 与
与 、
、 均相切,切点分别为(
均相切,切点分别为( )、(
)、( ),且
),且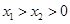 ,求证:
,求证: .
.(Ⅰ) 关于直线 对称;(Ⅱ)见解析;(Ⅲ)见解析.
对称;(Ⅱ)见解析;(Ⅲ)见解析.
 对称;(Ⅱ)见解析;(Ⅲ)见解析.
对称;(Ⅱ)见解析;(Ⅲ)见解析.试题分析:(Ⅰ)原函数与其反函数的图像关于直线
 对称;(Ⅱ)先求出反函数的解析式:
对称;(Ⅱ)先求出反函数的解析式: ,引入中间函数
,引入中间函数 .先构造函数
.先构造函数 ,利用函数的单调性与导数的关系,求得函数的最小值是
,利用函数的单调性与导数的关系,求得函数的最小值是 ,找到关系
,找到关系 ;再构造函数
;再构造函数 ,利用函数的单调性与导数的关系,求得函数的最小值是
,利用函数的单调性与导数的关系,求得函数的最小值是 ,找到关系
,找到关系 .从而证得“
.从而证得“ 的图象恒在
的图象恒在 的图象的上方”;(Ⅲ)先求出
的图象的上方”;(Ⅲ)先求出 以及
以及 ,根据导数与切线方程的关系,由斜率不变得到
,根据导数与切线方程的关系,由斜率不变得到 ,再根据两点间的斜率公式得到
,再根据两点间的斜率公式得到 .首先由指数函数的性质可得
.首先由指数函数的性质可得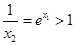 ,那么
,那么 ,然后由
,然后由 得到
得到 ,解得
,解得 .
.试题解析:(Ⅰ)
 与
与 的图象关于直线
的图象关于直线 对称. 2分
对称. 2分(Ⅱ)
 ,设
,设 , 4分
, 4分令
 ,
,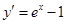 ,
,令
 ,解得
,解得 ,
,当
 时
时 ,当
,当 时
时 ;
;∴当
 时,
时, ,
,∴
 . 6分
. 6分令
 ,
, ,
,令
 ,解得
,解得 ;
;当
 时,
时, ,当
,当 时,
时, ,
,∴当
 时,
时, ,
,∴
 . 8分
. 8分∴
 的图象恒在
的图象恒在 的图象的上方. 9分
的图象的上方. 9分(Ⅲ)
 ,
, ,切点的坐标分别为
,切点的坐标分别为 ,可得方程组:
,可得方程组: 11分
11分∵
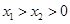 ,
,∴
 ,∴
,∴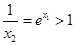 ,
,∴
 . 12分
. 12分由②得,
 ,∴
,∴ , 13分
, 13分∵
 ,∴
,∴ ,∴
,∴ ,即
,即 ,
,∴
 . 14分
. 14分
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.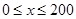 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).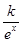 (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元. 为常数
为常数 .
.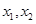 是关于
是关于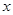 的方程
的方程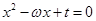 的两个根,且
的两个根,且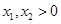 .
.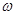 与
与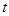 之间满足的关系式;
之间满足的关系式;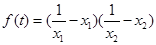 ,若存在
,若存在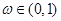 ,使不等式
,使不等式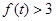 在其定义域范围内恒成立,求
在其定义域范围内恒成立,求 的解
的解 属于区间( )
属于区间( )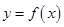 的图像是:( )
的图像是:( )
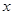 的方程
的方程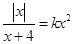 有四个不同的实数解,则
有四个不同的实数解,则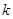 的取值范围为 ( )
的取值范围为 ( )



 ,在映射
,在映射 下
下 中与
中与 中元素
中元素 的对应元素为( )
的对应元素为( )


