题目内容

6．在△ABC中，∠CAB=∠CBA=30°，AC，BC边上的高分别为BD，AE，则以A，B为焦点，且过D，E两点的椭圆和双曲线的离心率的乘积为（　　）
A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$

分析 根据题意设出AB，进而根据椭圆的定义可求得a和c的关系式，求得椭圆的离心率．进而利用双曲线的性质，求得a和c关系，求得双曲线的离心率，然后求得椭圆和双曲线的离心率的乘积．

解答 解：设|AB|=2c，则在椭圆中，有c+$\sqrt{3}$c=2a，∴椭圆的离心率为$\sqrt{3}$-1，
而在双曲线中，有$\sqrt{3}$c-c=2a′，∴双曲线的离心率为$\sqrt{3}$+1，
∴椭圆和双曲线的离心率的乘积为（$\sqrt{3}$-1）（$\sqrt{3}$+1）=2
故选：C．

点评 本题主要考查了椭圆的简单性质和双曲线的简单性质．解题中灵活运用了椭圆、双曲线的简单性质．

练习册系列答案
相关题目
16．已知a＞0，b＞0．
（I）若a+b=2，求$\frac{1}{1+a}+\frac{4}{1+b}$的最小值；
（Ⅱ）求证：a2b2+a2+b2≥ab（a+b+1）．
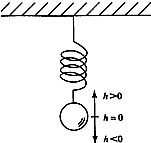17．如图，弹簧挂着的小球上下振动，时间t（s）与小球相对于平衡位置（即静止时的位置）的高度h（cm）之间的函数关系式是h=$\sqrt{2}$sint+$\sqrt{2}$cost，t∈[0，+∞）．，则小球开始振动时h的值为$\sqrt{2}$，小球振动时最大的高度差为4．
14．函数f（x）=sin2x+$\sqrt{2}cos（x+\frac{π}{4}）$的最大值是$\frac{5}{4}$．
1．已知函数f（x）=sinx•（2cosx-sinx）+cos2x．
（1）讨论函数f（x）在[0，π]上的单调性；
（2）设$\frac{π}{4}＜α＜\frac{π}{2}$，且$f（α）=-\frac{{5\sqrt{2}}}{13}$，求sin2α的值．
11．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（1，$\frac{\sqrt{3}}{2}$），离心率为$\frac{\sqrt{3}}{2}$．
（1）求椭圆C的方程；
（2）不垂直与坐标轴的直线l与椭圆C交于A，B两点，以AB为直径的圆过原点，且线段AB的垂直平分线交y轴于点P（0，-$\frac{3}{2}$），求直线l的方程．
18．设正项等比数列{an}满足a4a6=$\frac{1}{4}$，a7=$\frac{1}{8}$，则a1的值为（　　）
A．15B．14C．12D．8
15．如图，在正方体ABCD一A1B1C1D1中，AB=3，CE=2EC1．
（Ⅰ）若F是AB的中点，求证；C1F∥平面BDE；
（Ⅱ）求二面角D一BE一C的余弦值．
16．F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点，点P在双曲线右支上，△POF（O为坐标原点）满足OF=OP=$\sqrt{5}{，_{\;}}$PF=2，则双曲线的离心率为（　　）
A．$\sqrt{3}$B．2C．$\sqrt{5}$D．$\sqrt{3}$+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网