题目内容
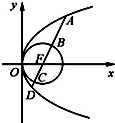
抛物线y2=4px（p＞0）上一点M到焦点的距离为a，则M到y轴距离为（ ）
| A．a-p | B．a+p | C．a-
| D．a+2p |
∵抛物线方程为y2=4px，p＞0
∴抛物线的焦点为F（p，0），准线方程为x=-p
根据抛物线的定义，点M到焦点的距离等于M到准线的距离，
∴|MF|=a=x+p，解之可得x=a-p，
即M到y轴距离为a-p．
故选：A
∴抛物线的焦点为F（p，0），准线方程为x=-p
根据抛物线的定义，点M到焦点的距离等于M到准线的距离，
∴|MF|=a=x+p，解之可得x=a-p，
即M到y轴距离为a-p．
故选：A
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
