题目内容
如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=______.
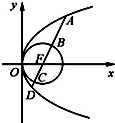

若直线的斜率不存在,则直线方程为x=1,代入抛物线方程和圆的方程,
可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),
所以AB=1,CD=1,
从而|AB•CD|=1.
若直线的斜率存在,设为k,则直线方程为y=k(x-1),因为直线过抛物线的焦点(1,0)
不妨设A(xa,ya),B(xb,yb),过AB分别作抛物线准线的垂线,由抛物线的定义,
|AF|=xa+1,|DF|=xb+1,
把直线方程与抛物线方程联立,消去y可得
k2x2-(2k2+4)x+k2=0,由韦达定理有 xaxb=1
而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|-|BF|=xa,|CD|=|DF|-|CF|=xb.
所以|AB•CD|=xaxb=1
故答案为:1
可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),
所以AB=1,CD=1,
从而|AB•CD|=1.
若直线的斜率存在,设为k,则直线方程为y=k(x-1),因为直线过抛物线的焦点(1,0)
不妨设A(xa,ya),B(xb,yb),过AB分别作抛物线准线的垂线,由抛物线的定义,
|AF|=xa+1,|DF|=xb+1,
把直线方程与抛物线方程联立,消去y可得
k2x2-(2k2+4)x+k2=0,由韦达定理有 xaxb=1
而抛物线的焦点F同时是已知圆的圆心,所以|BF|=|CF|=R=1
从而有|AB|=|AF|-|BF|=xa,|CD|=|DF|-|CF|=xb.
所以|AB•CD|=xaxb=1
故答案为:1

练习册系列答案
相关题目
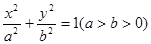 的右焦点为
的右焦点为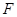 ,
,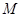 为上顶点,
为上顶点,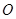 为坐标原点,若△
为坐标原点,若△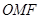 的面积为
的面积为 ,且椭圆的离心率为
,且椭圆的离心率为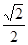 .
. 交椭圆于
交椭圆于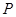 ,
,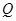 两点, 且使点
两点, 且使点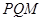 的垂心?若存在,求出直线
的垂心?若存在,求出直线