题目内容
【题目】已知抛物线C：
=2px经过点
（1，2）．过点Q（0，1）的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N．
（Ⅰ）求直线l的斜率的取值范围；
（Ⅱ）设O为原点，
，
，求证：
为定值．
【答案】(1) 取值范围是（-∞，-3）∪（-3，0）∪（0，1）
(2)证明过程见解析
【解析】分析：（1）先确定p,再设直线方程，与抛物线联立，根据判别式大于零解得直线l的斜率的取值范围，最后根据PA，PB与y轴相交，舍去k=3，（2）先设A（x1，y1），B（x2，y2），与抛物线联立，根据韦达定理可得
，
．再由
，
得
，
．利用直线PA，PB的方程分别得点M，N的纵坐标，代入化简
可得结论.
详解：解：（Ⅰ）因为抛物线y2=2px经过点P（1，2），
所以4=2p，解得p=2，所以抛物线的方程为y2=4x．
由题意可知直线l的斜率存在且不为0，
设直线l的方程为y=kx+1（k≠0）．
由
得
．
依题意
，解得k<0或0<k<1．
又PA，PB与y轴相交，故直线l不过点（1，-2）．从而k≠-3．
所以直线l斜率的取值范围是（-∞，-3）∪（-3，0）∪（0，1）．
（Ⅱ）设A（x1，y1），B（x2，y2）．
由（I）知
，．
直线PA的方程为y–2=
．
令x=0，得点M的纵坐标为
．
同理得点N的纵坐标为
．
由，得
，
．
所以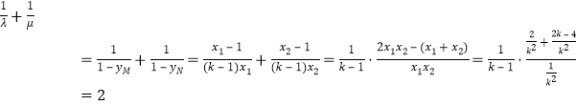
．
所以为定值．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
