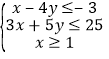题目内容
【题目】某厂生产
产品的年固定成本为250万元，每生产
千件需另投人成本
万元.当年产量不足80千件时，
（万元）；当年产量不小于80千件时，
万元，每千件产品的售价为50万元，该厂生产的产品能全部售完.
（1）写出年利润
万元关于千件的函数关系式；
（2）当年产量为多少千件时该厂当年的利润最大？
【答案】（1）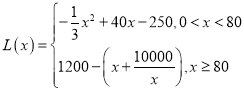
（2）100
【解析】
（1）由于每生产
千件需另投人成本受产量的影响有变化，根据题意，所以分当
时和当
时，两种情况进行讨论，然后根据利润的定义写出解析式.
（2）根据（1）的利润函数为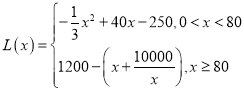，当时，用二次函数法求最大值；当时，用基本不等式求最大值.最后两段中取最大的为利润函数的最大值，相应的x的取值即为此时最大利润时的产量.
（1）根据题意
当时， 
，
当时， 
，
综上： .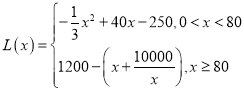
（2）由（1）知，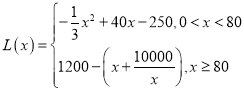
当时， 
，
当
时，
的最大值为950万.
当时， 
，
当且仅当
即
时取等号，的最大值为1000万.
综上：当产量为100千件时，该厂当年的利润最大.
练习册系列答案
小学课时特训系列答案
相关题目
