题目内容
5.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,以原点为圆心,椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切.(1)求椭圆C的方程;
(2)直线x=my+2与椭圆C交于A、B两点,E(-$\frac{2}{m}$,$\frac{m-2}{m}$),设△AEB的面积为S,若0<S≤1,求m的取值范围.
分析 (1)由椭圆的离心率得到a2=2b2,再根据椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切求得b,则椭圆方程可求;
(2)将直线的方程与椭圆方程联立,利用弦长公式求得|AB|,再求出E到直线AB的距离为d,代入三角形面积后由0<S≤1求得m的取值范围.
解答 解:(1)∵e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,∴e2=$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{2}$,即a2=2b2,
又∵b=$\frac{\sqrt{2}}{\sqrt{1+1}}$=1,
∴椭圆方程为:$\frac{x2}{2}$+y2=1;
(2)将直线的方程x=my+2代入$\frac{{x}^{2}}{2}$+y2=1得:(2+m2)x2-8x+8-2m2=0,
∴△=64-8(2+m2)(4-m2)=8m2(m2-2)>0,即m2>2.
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{8}{2+{m}^{2}}$,x1x2=$\frac{8-2{m}^{2}}{2+{m}^{2}}$,
∴|AB|=$\sqrt{1+\frac{1}{{m}^{2}}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+\frac{1}{{m}^{2}}}•\sqrt{(\frac{8}{2+{m}^{2}})^{2}-4•\frac{8-2{m}^{2}}{2+{m}^{2}}}$
=$\frac{\sqrt{1+{m}^{2}}}{|m|}•\frac{2\sqrt{2}|m|\sqrt{{m}^{2}-2}}{2+{m}^{2}}$=$\frac{2\sqrt{2}•\sqrt{1+{m}^{2}}\sqrt{{m}^{2}-2}}{2+{m}^{2}}$,
设E到直线AB的距离为d,则d=$\frac{|-\frac{2}{m}-m•\frac{m-2}{m}-2|}{\sqrt{{m}^{2}+1}}=\frac{2+{m}^{2}}{|m|•\sqrt{1+{m}^{2}}}$,
∴S=$\frac{1}{2}$•|AB|•d=$\frac{1}{2}$•$\frac{2\sqrt{2}•\sqrt{1+{m}^{2}}•\sqrt{{m}^{2}-2}}{2+{m}^{2}}•\frac{2+{m}^{2}}{|m|•\sqrt{{m}^{2}+1}}$=$\sqrt{2}•\frac{\sqrt{{m}^{2}-2}}{|m|}$.
由题意:0<$\sqrt{2}•\frac{\sqrt{{m}^{2}-2}}{|m|}$≤1,解得:2<m2≤4
∴m 的取值范围是[-2,-$\sqrt{2}$)∪($\sqrt{2}$,2]
点评 本题考查椭圆方程的求法,考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是压轴题.

| A. | (-1,0) | B. | (1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(1,+∞) |
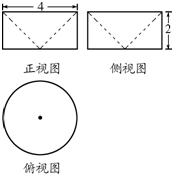
| A. | $\frac{8}{3}$π | B. | $\frac{16}{3}$π | C. | 8π | D. | 16π |
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$). 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PA=$\sqrt{6}$,M为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PA=$\sqrt{6}$,M为PC的中点.