题目内容
6.已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(-ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为$\frac{\sqrt{π}}{2}$.分析 由两角和的正弦函数公式化简解析式可得f(x)=$\sqrt{2}$sin(ωx+$\frac{π}{4}$),由2kπ-$\frac{π}{2}$≤ωx+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:-ω≥$\frac{2kπ-\frac{3π}{4}}{ω}$①,ω≤$\frac{2kπ+\frac{π}{4}}{ω}$②,k∈Z,从而解得k=0,又由ωx+$\frac{π}{4}$=kπ+$\frac{π}{2}$,可解得函数f(x)的对称轴为:x=$\frac{kπ+\frac{π}{4}}{ω}$,k∈Z,结合已知可得:ω2=$\frac{π}{4}$,从而可求ω的值.
解答 解:∵f(x)=sinωx+cosωx=$\sqrt{2}$sin(ωx+$\frac{π}{4}$),
∵函数f(x)在区间(-ω,ω)内单调递增,ω>0
∴2kπ-$\frac{π}{2}$≤ωx+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间为:[$\frac{2kπ-\frac{3π}{4}}{ω}$,$\frac{2kπ+\frac{π}{4}}{ω}$],k∈Z,
∴可得:-ω≥$\frac{2kπ-\frac{3π}{4}}{ω}$①,ω≤$\frac{2kπ+\frac{π}{4}}{ω}$②,k∈Z,
∴解得:0<ω2≤$\frac{3π}{4}-2kπ$且0<ω2≤2k$π+\frac{π}{4}$,k∈Z,
解得:-$\frac{1}{8}$$<k<\frac{3}{8}$,k∈Z,
∴可解得:k=0,
又∵由ωx+$\frac{π}{4}$=kπ+$\frac{π}{2}$,可解得函数f(x)的对称轴为:x=$\frac{kπ+\frac{π}{4}}{ω}$,k∈Z,
∴由函数y=f(x)的图象关于直线x=ω对称,可得:ω2=$\frac{π}{4}$,可解得:ω=$\frac{\sqrt{π}}{2}$.
故答案为:$\frac{\sqrt{π}}{2}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,正确确定k的值是解题的关键,属于中档题.

(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
| W | 12 | 15 | 18 |
| P | 0.3 | 0.5 | 0.2 |
(1)求Z的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
| A. | 若t确定,则b2唯一确定 | B. | 若t确定,则a2+2a唯一确定 | ||
| C. | 若t确定,则sin$\frac{b}{2}$唯一确定 | D. | 若t确定,则a2+a唯一确定 |
| A. | ρ=sin($\frac{π}{3}$+θ)+1 | B. | ρ=sin($\frac{π}{3}$-θ)+1 | C. | ρ=sin($\frac{π}{6}$+θ)+1 | D. | ρ=sin($\frac{π}{6}$-θ)+1 |
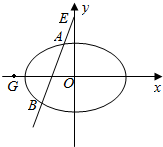 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.