题目内容
【题目】已知![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,当三棱锥
,当三棱锥![]() 体积最大时,其外接球的表面积为__________.
体积最大时,其外接球的表面积为__________.
【答案】![]()
【解析】
当三棱锥![]() 体积最大时,分析得出点C的位置,再根据球的性质,在直角三角形中解出球的半径,从而求得球的表面积.
体积最大时,分析得出点C的位置,再根据球的性质,在直角三角形中解出球的半径,从而求得球的表面积.
解:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
设![]() 的外接圆的圆心为
的外接圆的圆心为![]() ,
,![]() 的外接圆的圆心为
的外接圆的圆心为![]() ,
,
因为![]() 是边长为2的等边三角形,
是边长为2的等边三角形,
所以![]() 面积确定,
面积确定,
要使三棱锥![]() 体积最大,
体积最大,
即要使点![]() 到平面
到平面![]() 的距离最大,
的距离最大,
只有当平面![]() 平面
平面![]() 时,体积最大,
时,体积最大,
即点![]() 到边
到边![]() 的距离最大,三棱锥的体积最大,
的距离最大,三棱锥的体积最大,
因为![]() ,且
,且![]() ,
,
![]() 外接圆
外接圆![]() 的半径
的半径![]() 为
为![]() ,
,
所以点![]() 在
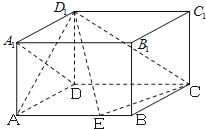
在![]() 外接圆上运动,如图所示
外接圆上运动,如图所示

当点![]() 满足
满足![]() 时,点
时,点![]() 到边
到边![]() 的距离最大,三棱锥的体积最大.
的距离最大,三棱锥的体积最大.
此时三棱锥的高即为![]() 的长,
的长,
此时![]() 外接圆
外接圆![]() 的圆心
的圆心![]() 在
在![]() 上,
上,
根据球的性质可知,![]() ,
,![]() ,
,![]()
故四边形![]() 为矩形,
为矩形,
故![]() ,
,
在![]() 中,球的半径平方为
中,球的半径平方为![]() ,
,
所以球的表面积为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:℃),对某种鸡的时段产蛋量
(单位:℃),对某种鸡的时段产蛋量![]() (单位:
(单位: ![]() )和时段投入成本
)和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根据散点图判断, ![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |